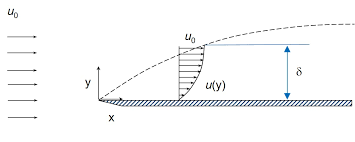
The thickness of the boundary layer ,`del`, can be defined as that distance from the boundary in which the velocity reaches 99% of the velocity of the free stream. This definition however gives the approximate thickness of the boundary layer and is generally termed as nominal thickness of boundary layer.
The commonly accepted definition of boundary layer thickness are:
ā?¢ Displacement thicknessĀ
ā?¢ Momentum thicknessĀ
ā?¢ Energy thicknessĀ
Displacement Thickness:Ā
Displacement thickness can be defined as the distance, measured perpendicular to the boundary of the solid body, by which the boundary should be displaced to compensate for the reduction in flow rate of the flowing fluid on account of the boundary layer formation.
Let us consider a fluid of density `rho` flowing with velocity U approaches a stationary plate as shown in figure. Consider an elementary strip of thickness `dy` at a distance y from the plate as shown below. Let u be the velocity of fluid at this level.
Assuming unit width of the plate, the mass flowing per second through the elemental strip is, `=rho*u*dy`
If the plate was not there, then the mass flowing per second through the elemental strip is, `= rho*U*dy`
Thus the reduction in mass flowing per secondĀ through the elemental strip due to the introduction of plate is, `=rho*(U-u)*dy`
The differenceĀ (U-u) is called the velocity of defect.
Total reduction in mass flow rate due to the introduction of plate is,
=$\int_{0}^Ī“ Ļ(U-u)dy $.... (i)
Let the plate is displaced by a distance `delta^**` and the velocity of flow for the distanceĀ `delta^**` is equal to the velocity of the free stream i.e, U. Then, the totalĀ mass of the fluid flowing per second through the distance `delta^**` is,
`=rho*U*delta^**`ā?¦ā?¦(ii)
Now equating (i) and (ii), we get,
`rho*U*delta^**=\int_{0}^Ī“ Ļ(U-u)dy`
$Ī“^*= \int_{0}^Ī“ Ļ(1-u/U)dy$
Momentum Thickness:Ā Ā
Momentum thickness can be defined as the distance, measured perpendicular to the boundary of the solid body, by which the boundary should be displaced to compensate for the reduction in momentumĀ of the flowing fluid on account of the boundary layer formation.
Let us consider a fluid of density `rho` flowing with velocity U approaches a stationary plate as shown in figure. Consider an elementary strip of thickness `dy` at a distance y from the plate as shown below. Let u be the velocity of fluid at this level.
Assuming unit width of the plate, the mass flowing per second through the elemental strip is, `=rho*u*dy`
The momentum per second of fluid inside the elementary area isĀ
`rho*u*dy*u=rho*u^2dy`
Momentum per second of sake mass of fluid before entering the boundary layer is,
`rho*u*dy*U= rho*uUdy`
Loss of momentum per second in elementary area due to the introduction of plate is,
`=rho*u*(U-u)dy`
Total loss of momentum per second due to the introduction of plate is ,
$\int_{0}^Ī“ Ļ \ u(U-u)dy$... (i)
Let `theta` be the distance by which the plate is displaced to compensate for the reduction in momentum and let U be the velocity of flow.
Then, the loss of momentum per second of the flowing fluid through the distance `theta` with velocity U is,
`=rho*theta*U^2`ā?¦(ii)
Now equating (i) and (ii), we get,
`rhothetaU^2=\int_{0}^Ī“ Ļ( u/U )(U-u)dy`
Or, `theta= \int_0^delta u/U (1-u/U)`
Energy Thickness:
Energy thickness can be defined as the distance, measured perpendicular to the boundary of the solid body, by which the boundary should be displaced to compensate for the reduction in K.E of the flowing fluid on account of the boundary layer formation.
Let us consider a fluid of density `rho` flowing with velocity U approaches a stationary plate as shown in figure. Consider an elementary strip of thickness `dy` at a distance y from the plate as shown below. Let u be the velocity of fluid at this level.
Assuming unit width of the plate, the mass flowing per second through the elemental strip is, `=rho*u*dy`
Kinetic energy of fluid inside the elementary area per second is, `1/2mu^2=1/2 (rho*u*dy)u^2`
If the plate was not there, then the kinetic energy of the flowing per second through the elemental strip is, `= Ā½ (rho*u*dy)U^2`
Thus the loss in kinetic energy of flowing fluid per secondĀ through the elemental strip due to the introduction of plate is, `=1/2rho u*(U^2-u^2)*dy`
Total loss of kinetic energy per secondĀ due to the introduction of plate is,
`=\int_{0}^Ī“ 1/2Ļu( U^2-u^2 )dy`ā?¦.(i)
Let the plate is displaced by a distance `delta_e` ro compensate for the reduction in kinetic energy and the velocity of flow for the distanceĀ `delta_e` is equal to the velocity of the free stream i.e, U. Then, the total kinetic energy of the fluid flowing per second through the distance `delta_e` is,
`=1/2 (rho*U*delta_e)U^2`ā?¦ā?¦(ii)
Now equating (i) and (ii), we get,
`1/2rho*delta_eU^2=\int_{0}^Ī“ 1/2Ļu( U^2-u^2 )dy`
Or, `delta_e= \int_0^delta u/U (1-u^2/U^2)dy`
 Guest
Guest