Chapter:
Hydrostatics--Buoyancy-and-metacentric-height
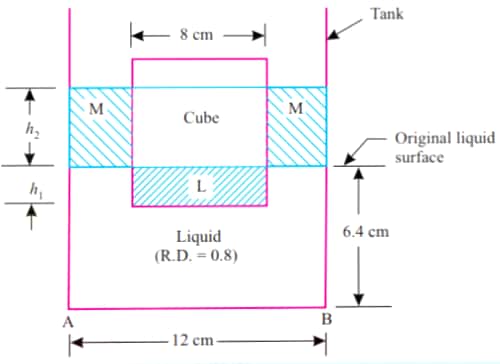
A 8 cm side cube weighing 4N is immersed in a liquid of relative density 0.8 contained in a rectangular tank of cross sectional area 12 cm ** 12 cm. If tank contains liquid to a height of 6.4 cm before immersion, determine levels of bottom of cube and liquid surface.
SOLUTION:
Given,
Side length of cube,`L=8 cm=0.08m`
Weight of cube, `W=4 N`
Relative density of liquid ,`S=0.8`
Let,
`h_1` be the height to which the bottom of the cube falls below original liquid level
`h_2` be the height of rise of liquid above the original liquid surface
Thus, `h_1 + h_2` will be the depth of submergence of the cube.
Now, from figure,
Volume L = volume Mâ?¦ (i)
Where,
Volume L = `8**8**h_1`
And....Show More
All Chapters
View all Chapter and number of question available From each chapter from Fluid-Mechanics
Dimensional Analysis, Similitude and Physical Modelling
Complete IOE exam solution including with important theory and numerical solution
Flow Past Through Submerged Body
Complete IOE solution including important theory and numericals
Boundary Layer Theory
Complete IOE exam solution and many important theory and numericals
Properties of fluid
- properties of fluids
- complete IOE solution on fluid mechanics
- Detailed description chapterwise
- Unlimited Numericals problem solved with updation daily
- And much more
Hydrostatics
- Hydrostatics basic theory
- All important Numericals
- IOE,PU, MIT,A.M.I.E,Delhi university,EUPS,Engineering service exam solved problems
- Detailed explanation
Hydrostatics- Buoyancy and metacentric height
- detailed explanation of force of buoyancy, metacentric height,stability of floating body
- unlimited numericals solved with updation weekly
- including IOE , PU, KU, GATE, MIT, ANNA UNIVERSITY,UPSC EXAM SOLUTIONS
- And much more
ORIFICES AND WEIRS
Complete IOE and GATE EXAM SOLUTION along with numerous Numericals from Fluid mechanics
Similar Question
This Chapter Hydrostatics--Buoyancy-and-metacentric-height consists of the following topics
 Guest
Guest