Chapter:
ORIFICES-AND-WEIRS-
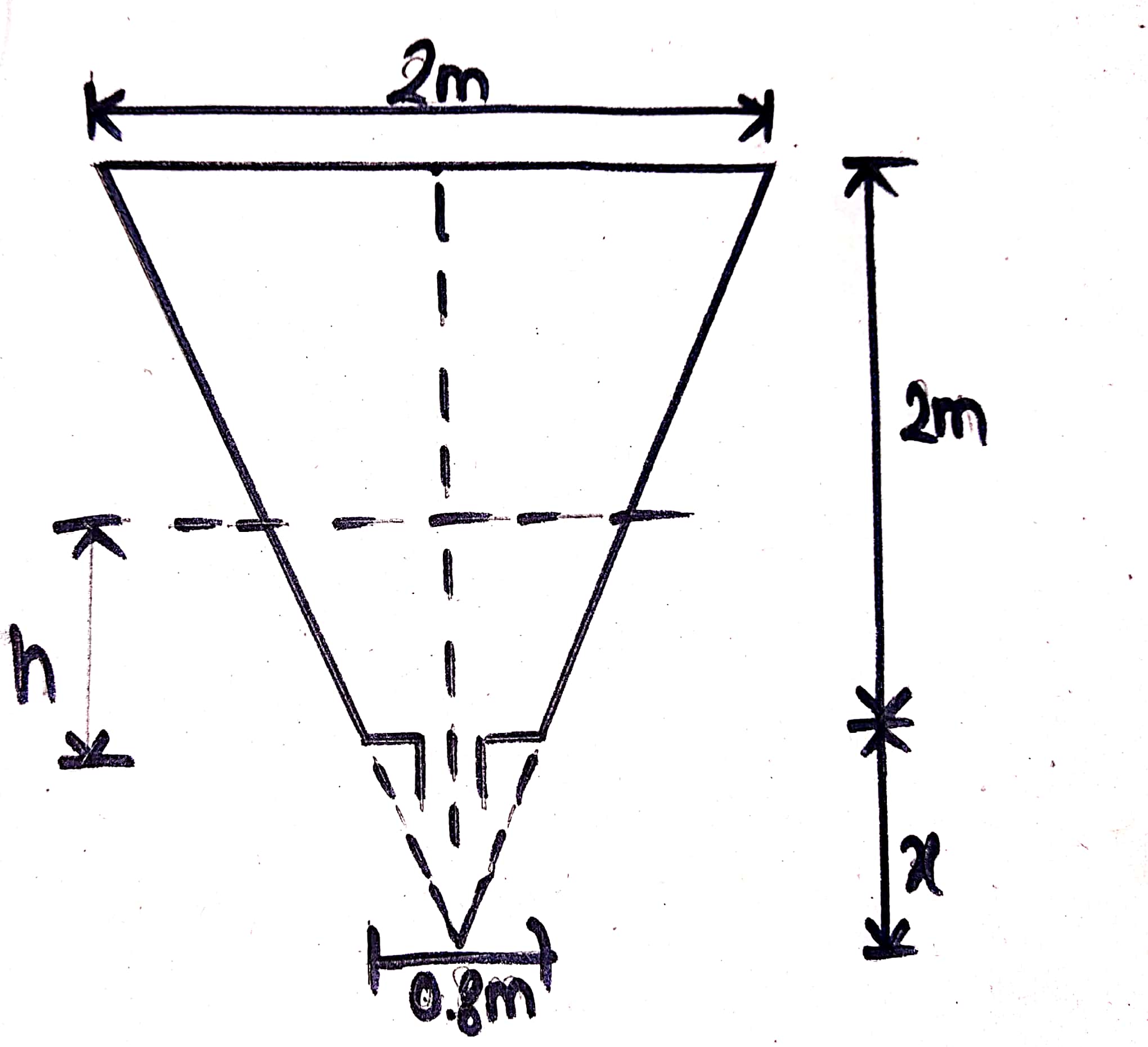
A tank is in form of a frustum of a cone having top diameter 2m, bottom diameter 0.8 m and height 2m and is full of water. Find time of emptying tank through orifice 100 mm in diameter at bottom. Take `C_d` as 0.625.
SOLUTION:
Here,
Area of orifice,`a=(pi**0.1^2)/4=0.0025pi \ m^2`
Let us consider any instant such that the height of water above the centre of orifice is h m. Let us say that during time `dT`, the level of water fall by`dh`. Let r be the radius of the liquid surface.
Now from the principle of continuity,
`-A*dh=C_d*a*root ()(2gh)*dT`
`-pir^2dh=C_d*a*root ()(2gh)*dT`... (i)
Now from figure,
`0.4/x=1/(2+x)`
or,`0.8+0.4x=x`
`x=4/3`
Also,
Show MoreAll Chapters
View all Chapter and number of question available From each chapter from Fluid-Mechanics
Dimensional Analysis, Similitude and Physical Modelling
Complete IOE exam solution including with important theory and numerical solution
Flow Past Through Submerged Body
Complete IOE solution including important theory and numericals
Boundary Layer Theory
Complete IOE exam solution and many important theory and numericals
Properties of fluid
- properties of fluids
- complete IOE solution on fluid mechanics
- Detailed description chapterwise
- Unlimited Numericals problem solved with updation daily
- And much more
Hydrostatics
- Hydrostatics basic theory
- All important Numericals
- IOE,PU, MIT,A.M.I.E,Delhi university,EUPS,Engineering service exam solved problems
- Detailed explanation
Hydrostatics- Buoyancy and metacentric height
- detailed explanation of force of buoyancy, metacentric height,stability of floating body
- unlimited numericals solved with updation weekly
- including IOE , PU, KU, GATE, MIT, ANNA UNIVERSITY,UPSC EXAM SOLUTIONS
- And much more
ORIFICES AND WEIRS
Complete IOE and GATE EXAM SOLUTION along with numerous Numericals from Fluid mechanics
Similar Question
This Chapter ORIFICES-AND-WEIRS- consists of the following topics
 Guest
Guest