Chapter:
1. Explain phase diagram of soil.
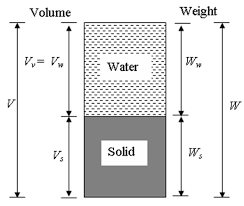
Soil mass is defined as the uncemented aggregate of minerals grains and decayed organic matter with liquid and gas in the empty spaces between the solid particles. The space between the soil particles is known as voids and these voids may be filled with either air or water or both.
The soil will behave as a two phase system when its space is filled with air or water alone. A two phase diagram either represent a dry or a completely saturated soil. When all void space is filled with water the soil mass is fully saturated and exist in two phases as solid and water . Similarly, when the soil mass is completely filled up by air, the soil mass becomes dry soil and exist in two phases is solid and air.
Fig: saturated soil- Two phase diagram.
Fig: dry soil- two phase diagram
When the soil mass is partially filled up by water as well as air, it will behave as a three phase system.
The diagrammatic representation of the different phases in a soil mass is called the Phase diagram.
Fig: unsaturated soil: three phase diagram
2. In an oil drilling project, a heavy viscous liquid ( drilling mud) was used to keep drilling hole open. It consists of suspension in water of following properties for litre of volume: `380` gm of clay of `G=2.82` `82` gm of sand of `G=2.68` `300` gm of iron filling of `G=7.13` Assuming that Unit Weight of water= `1` gram per cc and uniformly mixed suspension, what is unit weight of suspension?
`gamma=1.557(gm)/(cm^3)`
3.
Void ratio:
Void ratio is defined as the ratio of volume of voids to the volume of solid particles i.e,
`e=V_v/V_s`
`or, e=(V_w+V_a)/V_s`
Porosity:
Porosity denoted by n, is defined as the ratio of volume of voids to the total volume of soil. It is expressed in percentage.i.e,
`n=V_v/V*100`
`=(V_a+V_w)/(V_a+V_w+V_s)*100`
Degree of saturation:
Degree of saturation denoted by $S_r$ is defined as the ratio of volume of water to the total volume of voids in the soil mass. It is expressed in percentage.i.e,
`S_r=V_w/V_v*100`
Water content:
Water content or content of a soil mass, denoted by w, is defined as the ratio of weight of water to the weight of dry soil.i.e,
`w=W_w/W_s`
The weight used in the about expressions is the weight of water loss when the soil is heated to a temperature of 105 degree centigrade to 110 degree centigrade for such length of time that its weight is constant. In routing laboratory test, a period of 24 hours is considered enough for drying.
Bulk unit weight:
Bulk Unit Weight or mass unit weights denoted by `gamma_t` is defined as the weight of soil mass per unit volume of soil mass.i.e,
`gamma_t=W/V`
=`(W_s+W_w)/(V_s+V_w+V_a)`
Dry unit weight:
Dry Unit Weight denoted by `gamma_s` is defined as the ratio of weight of solid to volume of soil.i.e,
`gamma_s=W_s/V`
Unit weight of water:
It is the ratio of weight of water per unit volume of water.i.e,
`gamma_w=W_w/V_w`
Specific gravity of solids:
It is the ratio of Unit Weight of soil solid to Unit Weight of water at 4 degree centigrade.i.e,
`G=gamma_s/gamma_w`
`=W_s/(V_s*gamma_w)`
Specific gravityof water:
It is defined as the ratio of Unit Weight of water at any temperature to Unit Weight of water at 4 degree centigrade.i.e,
`G_t=gamma_w/gamma_0`
Where,`gamma_0` is the Unit Weight of water at 4 degree centigrade.
4. Prove `S_r *e=w*G`.
We know, the void ratio,e, is defined as a ratio of volume of voids to the volume of solid particles.
`e=V_v/V_s`
`=(V_v/V_w )*(V_w/V_s)`
`=(V_v/V_w)*((W_w/gamma_w)/(W_s/gamma_s))`
`=(V_v/V_w )*(W_w/W_s)*(gamma_s/gamma_w)`
We know,
Specific gravity,`G=gamma_s/gamma_w`
Thus,`e=(V_v/V_w)*(W_w/W_s)*G`
`=(1/S_r)*w*G`
Or, `S_r *e=w*G`
5. Prove: `gamma_t=(1+w)/(1+e)*G.gamma_w`
We know, by definition,
Bulk unit weight, `gamma_t=W/V`
Or,`gamma_t=(W_s+W_w)/(V_s+V_v )`
`=W_s/V_s* (1+W_w/W_s)/(1+V_v/V_s)`
`=gamma_s * (1+w)/(1+e)`
Thus, `gamma_t=gamma_s*(1+w)/(1+e)`
Again, we have,
Specific gravity,`G=gamma_s/gamma_w`
Thus,
`gamma_t=(1+w)/(1+e)*G.gamma_w`
6. Prove `gamma_t=(G+S_r*e)/(1+e)*gamma_w`
We know from above solution,
`gamma_t=(1+w)/(1+e)*G.gamma_w`..... (i)
Simalarly,we know,
`S_r*e=w*G`.... (ii)
Thus, `gamma_t=(G+S_r*e)/(1+e)*gamma_w`
Again,if the soil is saturate,then `S_r=1`,
So `gamma_t=gamma_(sat)` at `S_r=1`
Thus, `gamma_(sat)=(G+e)/(1+e)*gamma_w`
Again, if the soil is dry, then `S_r=0` and the bulk unit weight in this case becomes dry unit weight.
Thus, `gamma_d=G/(1+e)*gamma_w`
7. Prove: `gamma_d=gamma_t/(1+w)`
We know, by definition,
`gamma_d=W_s/V`
`=W_s/V*W/W`
`=(W/V)/((W_w+W_s)/W_s)`
`=gamma_t/(1+W_w/W_s)`
`=gamma_t/(1+w)`
Thus, `gamma_d=gamma_t/(1+w)`
8. Prove: `gamma_(sb)=(G-1)/(1+e)*gamma_w`.where,`gamma_(sb)` represents submerged unit weight.
By definition,we have,
`gamma_(sb )=gamma_(sat)-gamma_w`
Also,we know,
`gamma_(sat)=(G+e )/(1+e)*gamma_w`
Thus,`gamma_(sb)=((G+e)/(1+e)*gamma_w)-gamma_w`
`=(G+e-1-e)/(1+e)*gamma_w`
Thus, `gamma_(sb )=(G-1)/(1+e)*gamma_w`
9. Prove: `n=e/(1+e)`
We know,
`e=V_v/V_s`
Taking `V_s=1`,we get,
`e=V_v`
Now,
`V=V_v+V_s`
`=1+e`
Now, by definition,
`n=V_v/V`
`=e/(1+e)`
Thus,`n=e/(1+e)`
10. ` 1.` A `50` cc volume of moist soil weights `95` gram. It's dry weight is `75` gram and specific gravity of solid is `2.68`. Compute water content, void ratio, Porosity, and unit weight.
`w=26.7%`
`e=0.79`
`n=44%`
`gamma=1.9 (gm)/(cm^3)`
 Guest
Guest