Chapter:
1. Aerofoil
Aerofoil (Airfoil):
An airfoil or aerofoil is a streamlined body or a a structure with curved surfaces designed to give the most favourable ratio of lift to drag in flight, used as the basic form of the wings, fins, and tailplanes of most aircraft.
Some terms related to airfoil are:
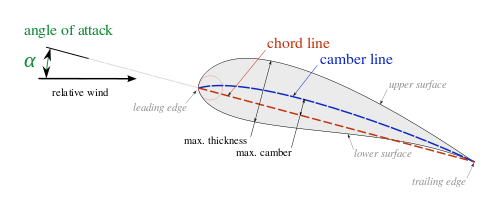
Aerofoil Section
Chord Line
Camber line
Angle of attack
Stall
Aspect ratio
Aerofoil Section:
The shape of a wing section is called aerofoil section.
Chord Line:
The line joining the leading and trailing edge of an airfoil is called chord and its length is called chord length.
Camber line:
The line connecting the mid-points of the upper and lower faces of the aerofoil section is called Camber line.
Angle of Attack:
It is the angle between the chord line and direction of the fluid stream.
Stall:
An airfoil is said to be in stall condition when the angle of attack of an airfoil is greater than the angle of attack at the minimum lift.
At stall, the air separates from the airfoil or wings and eddies are formed as a consequence of which there is a considerable increase in the drag coefficient.
Aspect Ratio:
The ratio of span of wing to its mean chord is called the aspect ratio.
I.e, A.R=`L/c`
Where, `L=`span of the wing
`C=` mean chord.
Since, `A=L*C`
`C=A/L`
Thus, A.R`=L^2/A`
We know the lift force is,
`F_l=rho*L*U*gamma`
Where, `gamma=` circulation developed on airfoil
`gamma=pi c*U*sinalpha`
where,`c=` chord length
`alpha=`angle of attack
`U=` free stream velocity of an air foil.
Thus, `F_l=rhoL*U*picUsinalpha`
`F_l=pi rho cLU^2sinalpha`...(i)
The lift force is also given by,
`F_l=C_L*(rho*U^2)/2*A`
`F_l=C_L*(rho*U^2)/2*C*L`..(ii)
From (i) and (ii),
`C_L=2pisinalpha`
NOTE: when a flying object such as aeroplane is in steady state, then
Weight of aeroplane = lift force,
`W=C_l*(rho*U^2)/2*A`
Thrust developed by the engine = the drag force
2. Streamlined Body
Streamlined Body:
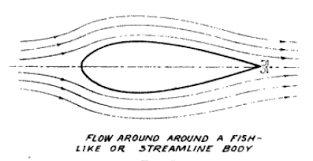
A streamlined body is a body having a shape that lowers the friction drag between a fluid, like air and water, and an object moving through that fluid. In other words, A streamlined body is defined as that body whose surface is aligned with the streamlines, when the body is placed in the flow.
Streamlined body experiences drag mainly due to Viscous/Frictional drag, which depends on the surface area exposed to fluid. Since the drag on the streamlined body is low, the lift/drag ratio is high.In this case, the separation usually takes place at the trailing edge.
An example of streamlined body is a thin aerofoil.
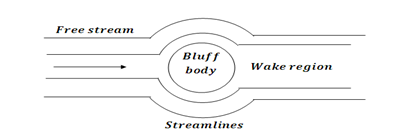
Bluff Body:
A bluff body is defined as that body whose surface is not aligned with the stream-lines, when placed in the flow. Thus, the body offers less resistance in terms of Viscous/Frictional drag. There is a very large pressure drag, due to eddy formation after the body leading to a large wake region. Thus the pressure drag depends on the cross sectional area of the body rather than the surface area exposed.
3. Derive an expression for forces acting on a submerged body.
A body wholly immersed in a real fluid may be subjected to the following two kinds of forces due to the relative motion between the body and fluid. These are:
Drag Force
Lift Force
Drag Force:
The component of force in the direction of flow (free stream) acting on a submerged body which tends to resist the motion is called drag force.Drag force is equal to Thrust force at steady condition of aircraft(When aircraft travelling with constant speed).
Lift Force:
The component of force at right angles to the direction of flow is called lift force.Lift is the force on the aircraft which is equal to weight force of the aircraft in steady condition. Lift is in vertically upward direction of the aircraft. This force keeps aircraft in the air.
Differences between drag and lift force:
S.NO | Drag Force | Lift Force |
1 | The component of force in the direction of flow (free stream) acting on a submerged body which tends to resist the motion is called drag force | The component of force at right angles to the direction of flow is called lift force. |
2 | It is possible to create drag without lift. | It is impossible to create drag without lift. |
3 | The drag force always exists. | The production of lift force requires assymmetry of flow. |
4 | Drag force is equal to Thrust force at steady condition of aircraft(When aircraft travelling with constant speed). | Lift force on the aircraft is equal to weight force of the aircraft in steady condition. |
Consider an arbitrary shaped solid body placed in a real fluid, which is flowing with a uniform velocity `U` in the horizontal direction as shown in figure. Let us consider a small elemental area `dA` on the surface of the body. Now, the forces acting on the small surface `dA` are:
Pressure force equal to `P*dA` acting perpendicular to the surface.
Shear force equal to `tau_0*dA` acting along the tangential direction to the surface.
Let `theta` be the inclination of the tangent to the element with the direction of flow.
Drag Force:
The component of force due to P and `tau_x` along the direction of motion is known as drag force.
Drag force on the elemental area= force due to pressure in the direction of flow + flow due to shear stress in teh direction of fluid motion.
`dF_d=P*dA*sintheta + tau_0dA*costheta`
Total drag force is,
`F_D=intP*dA*sintheta+inttau_0*dA*costheta`
Lift Force:
The component of force perpendicular to the direction of flow is called lift force.
Lift force on the elemental area= force due to pressure in the direction perpendicular to the direction of motion + flow due to shear stress in the direction perpendicular to the direction of motion
`dF_L=tau_0*dA*sintheta - P*dA*costheta`
Now, the total lift is,
`F_L=inttau_0*dA*sintheta-intP*dA*costheta`
The drag and lift for a body moving in a fluid of density `rho` at uniform velocity `U` are calculated as:
`F_D=C_D*(rho*U^2)/2*A`
and `F_L=C_L*(rho*U^2)/2*A`
Where, `C_D=` coefficient of drag
`C_L=` coefficient of life
`A=` characteristic area
For calculating drag force `F_D`, the area A is taken as area projected on the plane perpendicular to the relative motion of fluid.
For calculating the lift force `F_L`, the area A is taken as area projected on a plane at right angle to the direction of lift force.
In case of air foil, the projection is conventionally taken on the plane of the chord i.e, the area of wings itself, independent of its inclination to the direction of the flow.
area= span `l`* mean chord `c `
4. Explain drag of a Cylinder.
Consider a real fluid flowing past a cylinder of length L and diameter D. the drag coefficient is,
`F_D=C_D*(rho*U^2)/2*A`
Where A is the projected area, which is equal to `LD` for a cylinder.
At very small velocities, `R_e<0.5` the fluid sticks to the cylinder all the way round and never separates from the cylinder. This produces a streamline pattern similar to that of an ideal fluid as shown in figure. The dynamic pressure is achieved at the front stagnation point and vacuum equal to the dynamic pressure exists at the top and bottom where the velocity is at its greatest.
As the velocity increases, the boundary layer breaks away and eddies are formed behind as shown in figure. The drag pressure increases at the front due to the pressure behind and drag pressure drops at the back.
A further increase in velocity cause eddies to elongate and the drag coefficient becomes nearly constant as shown in figure. The pressure distribution shows that ambient pressure exists at the rear of the cylinder.
At Reynolds number of around 90, the vortices break away alternatively from the top and bottom of the cylinder producing a vortex street in the wake as shown in figure. The pressure distribution shows the vacuum at the rear.
Drag Coefficient as a function of Reynolds Number:
For `R_e<1`the flow pattern will be symmetrical.
For `R_e =1 1 to 2000, `C_D` decreases and attains a minimum value of 0.95 at `R_e`=2000.
For `R_e=2000` to `3*10^4`, `C_D` increases and become 1.2 at `R_e=3*10^4`
For `R_e=3*10^4` to `3*10^5`, `C_D` decreases and its value becomes 0.3 at a value of `R_e=3*10^5`
For `R_e=3*10^6`, `C_D` increases and attains a value of o.7 in the end.
5. Explain drag of a Sphere.
Let us consider a case when real fluid flows past a sphere. Let D be the diameter of the sphere, v be the velocity of flow pf fluid of mass density `rho` and viscosity `mu`.
We have,
`R_e=(rho*U*D)/mu`
When velocity of flow is very small or the fluid is very viscous such that the Reynolds number is very small (`R_e<=0.2`), then the viscous forces are more predominant than the inertial force. Stokes analysed theoretically the flow around sphere under `R_e<0.2` and found that the total drag force is,
`F_D=3pimuDU`....(i)
He also found that out of total drag, two third is contributed by skin friction and one third by pressure difference.
Thus,
Skin friction drag`=2/3F_D=2pimuDU`
Pressure drag `=1/2F_d=pimuDU`
Again, the total drag is,
`F_D=C_D*(rho*U^2)/2*A`
Where `A` is the projected area of sphere.
`A=(pi*D^2)/4`
Thus,
`C_D*(rho*U^2)/2*A=3pimuDU`
`C_D=(24mu)/(rhoUD)=24/R_e`
For `R_e` between 0.2 and 5
`C_D=24/R_e(1+3/(16R_e))` this is called onseen formula.
For `R_e` between 5 and 1000, `C_D=0.4`
For `R_e` between 1000 and 100,000, `C_D=0.5`.
For `R_e>10^5`, `C_D=0.2`.
6. Define aerofoil with accepted terminology with neat sketch. A kite which may be assumed to be a flat plate and mass 1 kg soars at an angle to horizontal. The tension in string holding kite is 60N when wind velocity is 50 km/hr horizontally and angle of string to horizontal direction is `35^0`. The density of air is 1.2 kg/`m^3`. Calculate drag coefficient for kite in given position if lift coefficient in same position is 0.45. Both coefficients have been used in full area of kite. [ 2068-Shrawan ][8]
7. A 2mm diameter spherical ball of unit weight 117.5 KN/`m^3` is dropped in a mass of fluid of viscosity 15 poise and specific gravity 0.95. Find out drag force, skin drag and terminal velocity of ball. [2068-Chaitra ][8]
8. A jet plane having a wing area of `30 m^2` and weighing 28 KN flies at 900 km/hr. The engine develops 8000 KW and has a mechanical efficiency of 70%. Determine lift and drag coefficient for wind taking density of air as 1.2 kg/`m^3`. [2069-Chaitra ][4]
9. Given: Military aircraft with M=8000 kg, lands on 350 km/hr and is slowed by a parachute with `A=10 m^2` area. Find
- Estimate time needed to slow to 200 km/hr.
- Maximum deceleration rate.
Model chute as an open hemisphere. [2070-Chaitra ][8]
10. A kite has an effective area of `0.6 m^2` and mass 0.4 kg. It experience a drag of 15 N in a wind speed of 40 km/hr. Determine
- tension in chord if it makes an angle of `45^0` with horizontal.
- lift coefficient for kite
Consider density of air as 1.2 kg/`m^3`. [2070-Ashad ][8]
All Chapters
Dimensional Analysis, Similitude and Physical Modelling
Flow Past Through Submerged Body
Boundary Layer Theory
Properties of fluid
- properties of fluids
- complete IOE solution on fluid mechanics
- Detailed description chapterwise
- Unlimited Numericals problem solved with updation daily
- And much more
Hydrostatics
- Hydrostatics basic theory
- All important Numericals
- IOE,PU, MIT,A.M.I.E,Delhi university,EUPS,Engineering service exam solved problems
- Detailed explanation
Hydrostatics- Buoyancy and metacentric height
- detailed explanation of force of buoyancy, metacentric height,stability of floating body
- unlimited numericals solved with updation weekly
- including IOE , PU, KU, GATE, MIT, ANNA UNIVERSITY,UPSC EXAM SOLUTIONS
- And much more
 Guest
Guest