Guest
You need to login to ask any Questions from chapter hydrostatics-buoyancy-and-metacentric-height of fluid-mechanics

Chapter:

hydrostatics-buoyancy-and-metacentric-height

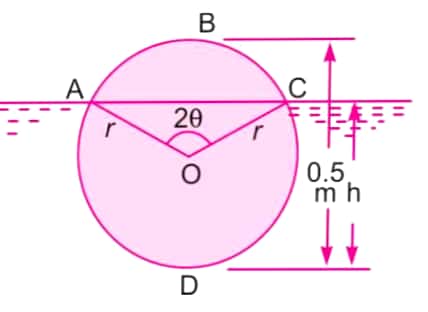
1. A wooden log of 0.6 m diameter and 5m in length is floating in river water. Find depth of wooden log in water when specific gravity of log is 0.7.

SOLUTION:

Given,

Diameter of wooden log, `D=0.6 m`

Length of log,`L=5 m`

Specific gravity of log,`S=0.7`

A wooden log of 0.6 m diameter and 5m in length is floating in river water. Find the depth of the wooden log in water when the specific gravity of the log is 0.7.

Here,

Weight of wooden log `=V*rhog`

`=A*L*rhog`

`=pi/4**0.6^2**5**0.7**1000**9810`

`=9707.99 N`

Now, for equilibrium,

Weight of wooden log = weight of water displaced

=Volume of water displaced ** weight density

or, volume of water displaced `=9707.99/(9.81**1000)`

`=0.9896 m^3`

Let h be the depth of immersion.

Now,

Volume of log inside water = volume of water displaced

or, area of ACDA ** Length =0.9896

or, area of sector OADC + area of `triangle AOC` = `0.9896/5`

or,`pi**0.3^2**(180+2theta)/360+½*rsintheta*(rcostheta+rcostheta)=0.9896/5`

Solving this, we get,

`theta=18.64^0`

Again from figure,

`h=r+rsintheta`

`=0.3959 m`

2. A metallic cube 30 cm side and weighing 450 N is lowered into a tank containing a two layer fluid of water and mercury. Determine position of block at mercury-water interface at equilibrium condition. [ANNA UNIVERSITY ]

$A metallic cube 30 cm side and weighing 450 N is lowered into a tank containing a two layer fluid of water and mercury. Determine the position of block at mercury-water interface at equilibrium condition.\r\n[ANNA UNIVERSITY ]$

SOLUTION:

Given,

Side length of cube,`L=30 cm=0.3m`

Weight of metallic cube, `W=450 N`

Now, From the principle of floatation,

Weight of cube = Buoyant force

=weight of water and mercury displaced by the block

or,`W=V_w*gamma_w+V_m*gamma_m`

or,`450=(0.3**0.3**h_1)**9810+13600**9.81**(0.3**0.3**h_2)`

or,`450=0.3**0.3**9.81**1000 (h_1+13.6h_2)`

or,`h_1+13.6h_2=0.5097`.... (i)

Again,from figure,

`h_1+h_2=0.3`.... (ii)

Solving equations (i) and (ii), we get,

`h_1=0.283 m`

`h_2=0.01658 m`

Thus,the block is 0.01658 m below the interface.

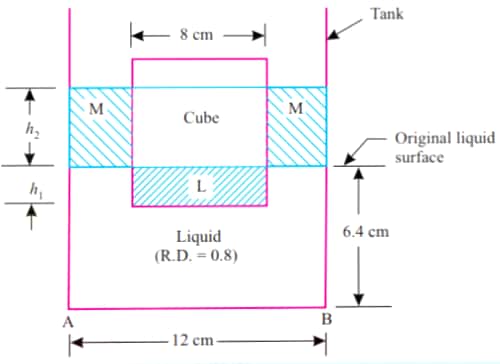
3. A 8 cm side cube weighing 4N is immersed in a liquid of relative density 0.8 contained in a rectangular tank of cross sectional area 12 cm ** 12 cm. If tank contains liquid to a height of 6.4 cm before immersion, determine levels of bottom of cube and liquid surface.

SOLUTION:

Given,

Side length of cube,`L=8 cm=0.08m`

Weight of cube, `W=4 N`

Relative density of liquid ,`S=0.8`

A 8 cm side cube weighing 4N is immersed in a liquid of relative density 0.8 contained in a rectangular tank of cross sectional area 12 cm ** 12 cm. If the tank contains liquid to a height of 6.4 cm before the immersion, determine the levels of the bottom of the cube and the liquid surface.

Let,

`h_1` be the height to which the bottom of the cube falls below original liquid level

`h_2` be the height of rise of liquid above the original liquid surface

Thus, `h_1 + h_2` will be the depth of submergence of the cube.

Now, from figure,

Volume L = volume M�?� (i)

Where,

Volume L = `8**8**h_1`

And volume M = `12**12**h_2-8**8**h_2` (see figure)

Thus from equation (i),

or,`8**8**h_1=12**12**h_2-8**8**h_2`

or,`h_1=1.25h_2`... (ii)

Also, From the law of floatation,

Weight of cube = Buoyant force

=weight of water displaced by immersed portion

or,`4=0.8**9.81**1000**8**8 (h_1+h_2)**10^(-6)`

or,`h_1+h_2=7.9638`... (iii)

Now, from equations (ii) and (iii),

`h_1=4.424 cm`

`h_2=3.5395 cm`

Thus the level of cube above BC is

`=6.4-4.424`

`=1.976 cm`

Also the level of liquid surface above plane BC is,

`=6.4+3.5395`

`=9.94 cm`

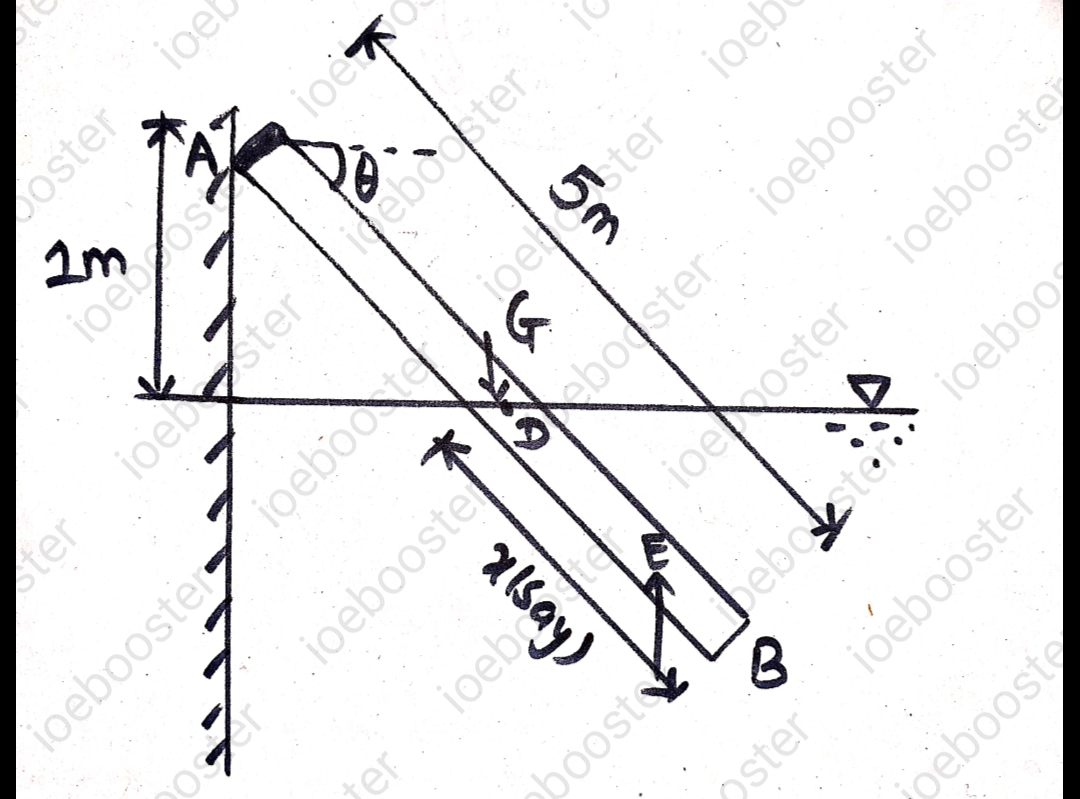
4. The wooden beam shown in figure is 200 mm 200 mm 5 m long. It is hinged at A and remains in equilibrium at `ta` with horizontal. Find inclination `ta`. The specific gravity of wood can be taken as 0.70.

The wooden beam shown in figure is 200 mm ** 200 mm ** 5 m long. It is hinged at A and remains in equilibrium at `theta` with the horizontal. Find the inclination `theta`. The specific gravity of wood can be taken as 0.70.

SOLUTION:

Let, the specific weight of water `=w`

Thus, the specific weight of wood becomes `0.6w`

Let `x m` length of the beam is immersed under water as shown in figure.

Now, the weight of the beam acting at point G i.e, c.g. of the beam is,

`=V*rho*g`

`=0.2**0.2**5**0.6w`

`=0.12w`N

Similarly the upthrust on the wooden beam is,

`=V_(in)*rho_w*g`

`=0.2**0.2**x.w`

`=0.04 wx` N

This upthrust acts at point E i.e, at the point of centre of buoyancy.

`AG=5/2=2.5`

`AE=5-x/2`

Now, taking moments about the hinge A, we get,

`0.12w**2.5 costheta=0. 04 wx (5-x/2)costheta`

or,`0.3=0.20x-0.02x^2`

Solving this, we get,

`x=1.838 m`

Also,

`sintheta=1/(5-1.838)`

or,`theta=18^0 26'`

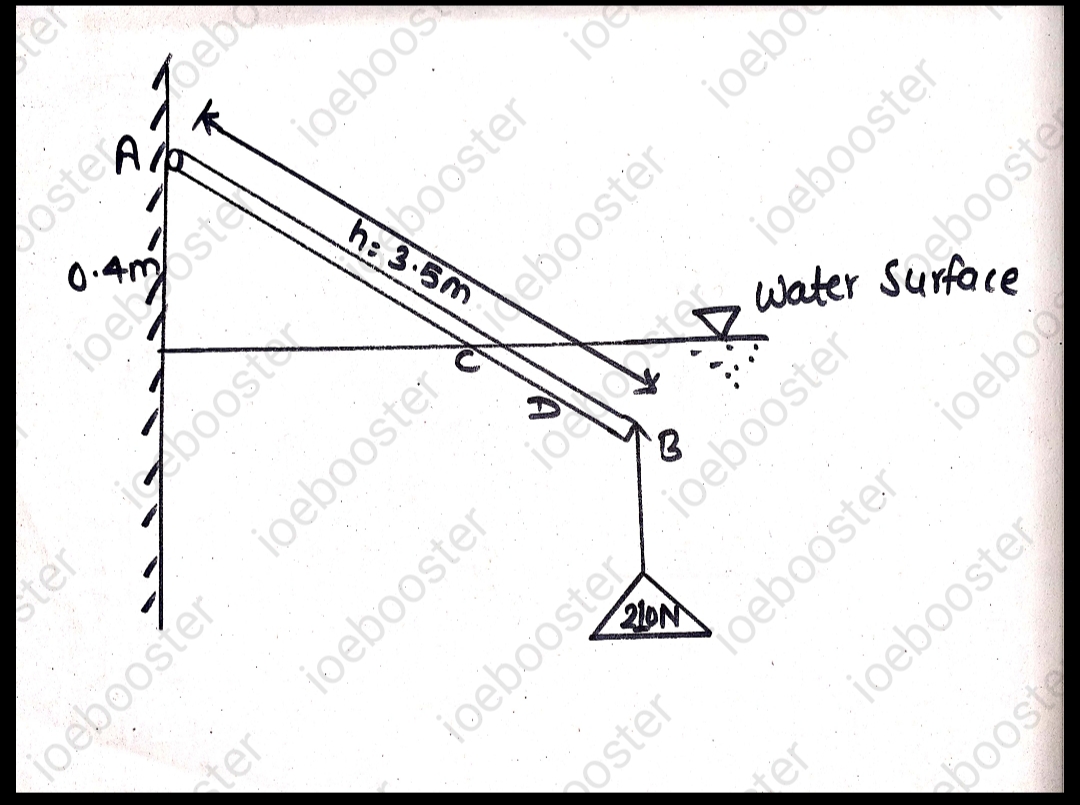
5. A wooden block of volume `0.03 m^3` weighing 210 N is attached to one end of a 3.5 m long wooden rod are under hinged to a wall. The block and part of rod are under water in position shown in figure. Find inclination `ta` of rod with horizontal. The rod weighs 15 N and has a uniform sectional area of 2000 `mm^2`.

A wooden block of volume `0.03 m^3` weighing 210 N is attached to one end of a 3.5 m long wooden rod are under hinged to a wall. The block and part of the rod are under water in the position shown in the figure. Find the inclination `theta` of the rod with the horizontal. The rod weighs 15 N and has a uniform sectional area of 2000 `mm^2`.

SOLUTION:

Here,

Weight of the wooden block =210 N

Weight of the rod = 15 N

Thus, the upthrust on block is,

`=V*rho*g`

`=0.03**1000**9.81`

`=294.3`

Similarly,the upthrust on rod is,

`=V_(i n)*rho*g`

`=2000**10^(-6)**1000**9.81**(3.5-0.4/(sintheta))`

`=19.62 (3.5-0.4/(sintheta))`

Now, taking moment about A, we get,

`294.3**3.5 costheta+19.62 (3.5-0.4/(sintheta))**1/2 (3.5+0.4/(sintheta))*costheta=210**3.5costheta+15**3.5/2costheta`

or,`1030.05+9.81 (12.25-0.16/(sin^2theta))=735+26.25`

Solving this,we get,

`theta=3^0 28'`

6. Two spheres weighing 10 KN and 25 KN are each 1.6 m in diameter. They are connected by a short rope and placed in water. Find tension in connecting rope. Find also what portion of lighter sphere will protrude above water surface.

SOLUTION:

Here,

Considering the lower sphere,

Buoyant force = net downward force

or,`4/3pi**0.8^3**9.81**1=25-T`

or,`T=3.958 KN`

Similarly, Considering the upper sphere,

Buoyant force = net downward force

or,`(V_(i\n)*rho_w*g)/1000=10+T`

or,`V_(i\n)**9.81=10+3.958`

`V_(i\n)=1.4228 m^3`

Thus the volume above water is,

`=V-V_(i\n)`

`=4/3 pi**0.8^3-1.4228`

`=0.722 m^3`

Now, the percentage of volume above water is,

`=0.722/2.145 **100%`

`=33.66%`

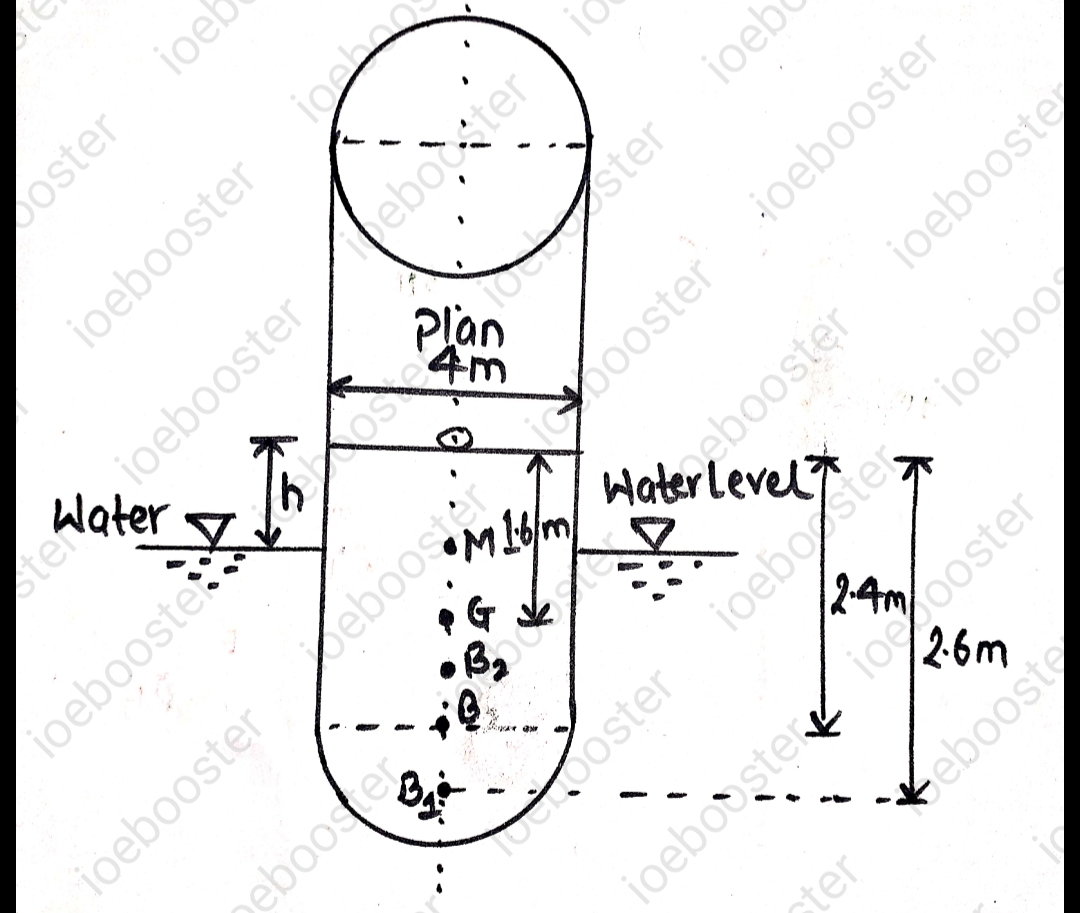
7. A body has cylindrical upper portion of 4m diameter and 2.4 m deep. The lower portion, which is curved; displaces a volume of 800 litres of water and its centre of buoyancy is situated 2.6m below top of cylinder. The centre of gravity of whole body is 1.6 m below top of cylinder and total displacement of water is 52 KN. Find metacentric height of body.

A body has the cylindrical upper portion of 4m diameter and 2.4 m deep. The lower portion, which is curved; displaces a volume of 800 litres of water and its centre of buoyancy is situated 2.6m below the top of cylinder. The centre of gravity of the whole body is 1.6 m below the top of the cylinder and the total displacement of water is 52 KN. Find the metacentric height of the body.

SOLUTION:

Given,

Volume of water displaced by the lower portion =800 L

`=0.8 m^3`

Also the total displacement of the water =52 KN

Thus the total volume of water displaced is`=52/9.81=5.3 m^3`

Hence the volume of water displaced by the upper cylindrical portion is`=5.3-0.8=4.5 m^3`

Let h be the distance between free surface of liquid from top of the body.

Volume of water displaced by upper portion`=pi/4**4^2**(2.4-h)`

or,`4.5=pi**4**(2.4-h)`

or,`h=2.04 m`

Now the distance of centre of buoyancy of the cylindrical portion from the top is,

`OB_2=h+(2.4-h)/2=2.22 m`

Let B be the centre of buoyancy of the whole body,

`OB=((Volume\ of\ Curved\ po rtion**OB_1)+(Volume\ of\ Cyl i ndrical\ po rtion**OB_2))/(Total\ Volume\ of\ water\ displaced)`

`=(0.8**2.6+4.5**2.22)/(0.8+4.5)`

`=2.277 m`

Now,

`BG=OB-OG`

`=2.277-1.6`

`=0.677 m`

Also,

`BM=I_(yy)/V`

Where,

`I_(yy)`=M.I of the plane of the body at the water surface.

or,`I_(yy)`=M.I of the cylindrical portion (top portion) about its c.g.

`=pi/64**4^2`

`=12.566 m^4`

And `V`=total volume of liquid displaced

or,`V=5.3 m^3`

Thus,

`BM=12.566/5.3`

`=2.37 m`

Hence the metacentric height is,

`GM=BM-BG`

`=2.37-0.677`

`=1.693 m`

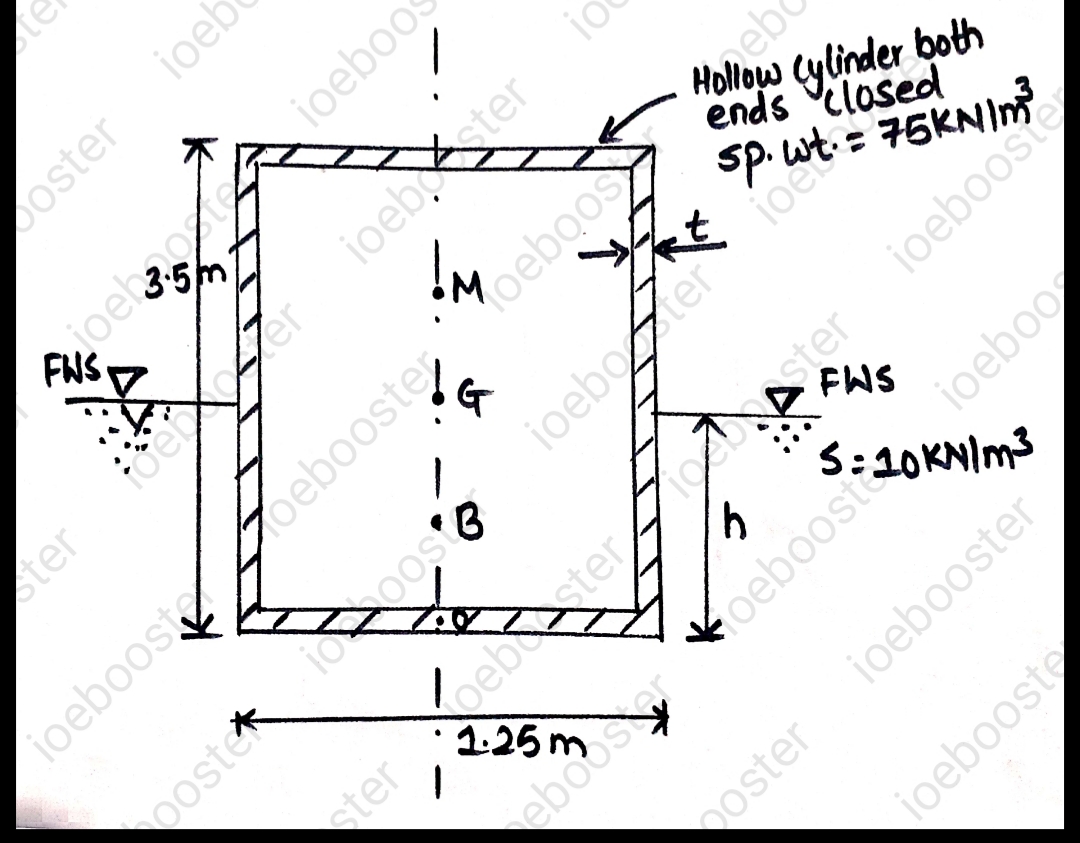
8. A hollow cylinder closed at both ends has an outside diameter of 1.25 m, length 3.5 m and specific weight 75 KN/`m^3`. If cylinder is to float just in stable equilibrium in sea water ( specific weight 10 KN/`m^3`), find its minimum permissible thickness.

A hollow cylinder closed at both ends has an outside diameter of 1.25 m, length 3.5 m and specific weight 75 KN/`m^3`. If the cylinder is to float just in stable equilibrium in sea water ( specific weight 10 KN/`m^3`), find its minimum permissible thickness.

SOLUTION:

Let,

h be the depth of immersion and t be the minimum possible thickness

Now, from the law of floatation,

Weight of cylinder = weight of water displaced

`V_(cyl i nder) **sp.weight=pi/4**1.25**h**10`

or,`(Volume\ of\ two\ end\ Section + Volume\ of\ Circ u lar Po rtion)*Sp.Wt.=pi/4**15.625h `

`{2**pi/4d^2t+pi/4 (d^2-(d-2t)^2)L}w_c=12.2718h`

Assuming `t < < L`

`{2**pi/4d^2t+pi/4 (d^2-(d^2-4dt+4t^2))L}w_c=12.2718h`

`{(pid^2t)/2+pi/4 (4dt)L}w_c=12.2718h`

`{(pi**1.25^2t)/2+pi**1.25tL}7.5=12.2718h`

`h=99t`

Now, Volume of seawater displaced is,

`V=((pi/2**1.25^2t+pi**1.25**t**3.5)7.5)/10`

`=121.5t`

Let M be the point ot metacentre.

Thus,

`BM=I_(yy)/V`

`=pi/64**1.25^4/(121.5t)`

`=0.00099/t`

`OB=h/2=49.5t`

`OG=3.5/2=1.75 m`

Now,

`BG=OG-OB`

`=1.75-49.5t`

Now for the cylinder to just float in stable equilibrium,

`GM=0`

or,`BM-BG=0`

`1.75-49.5t=0.00099/t`

Solving this we get two values of t as,

`t=0.03478` and `t=5.75**10^(-4)`

Clearly,

Minimum permissible thickness is, `t=5.75**10^(-4) m`

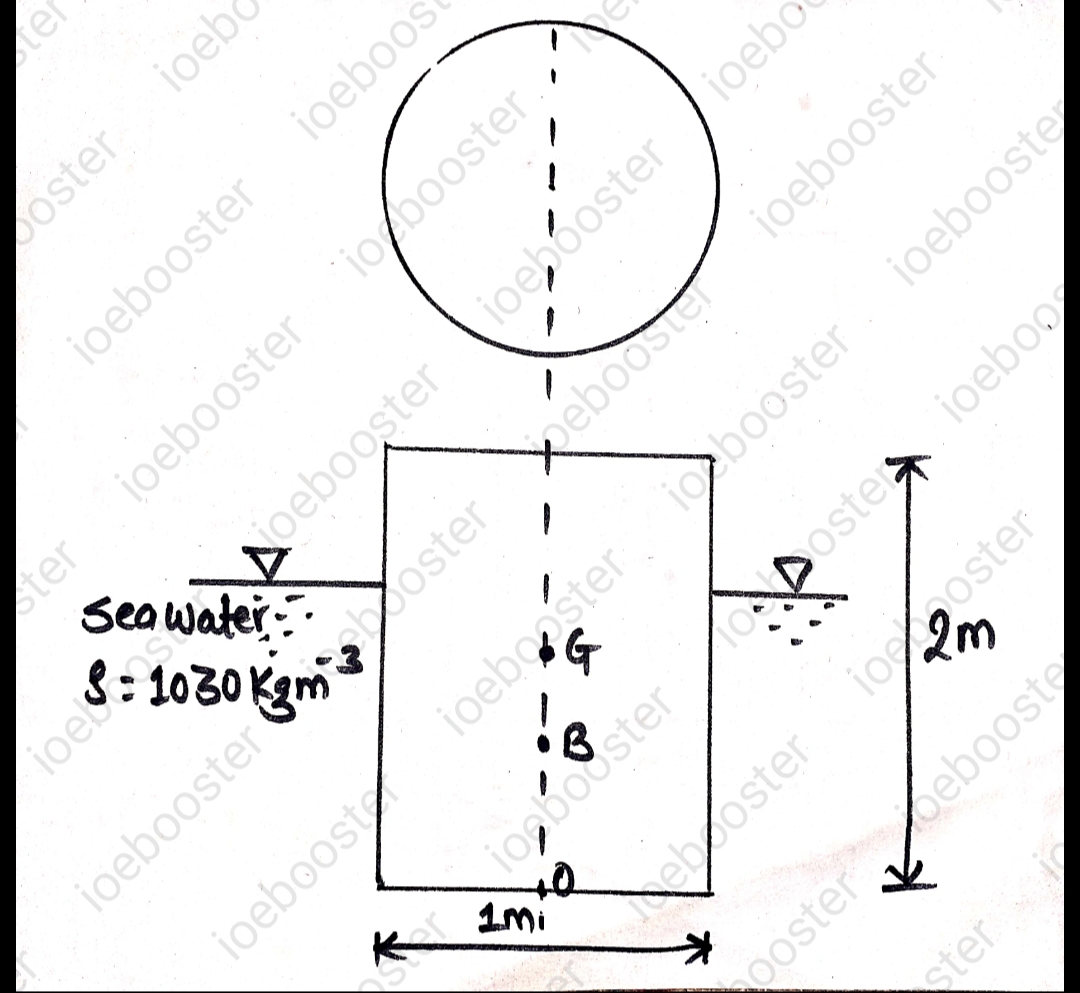
9. Show that a cylindrical buoy of 1m diameter and 2m height weighing 7.848 KN will not float vertically in sea water of density 1030 kg/`m^3`. Find force necessary in a vertical chain attached at centre of base of buoy that will keep it vertical.

Show that a cylindrical buoy of 1m diameter and 2m height weighing 7.848 KN will not float vertically in sea water of density 1030 kg/`m^3`. Find the force necessary in a vertical chain attached at the centre of the base of the buoy that will keep it vertical.

SOLUTION:

Let,

h be the depth of immersion

Now, from law of Floatation,

Weight of cylinder = Buoyant force

`7.848=(pi**1^2)/4**h**1030**9.81**1/1000`

`h=0.9899 m`

Now, the distance of c.g. from base is,`=2/2=1m`

Similarly, the distance of C.B. from base is,`=h/2=0.49479`

Now,

`BG=OG-OB`

`=0.50503`

Now the metacentric height is,

`GM=I _(yy)/V-BG`

Where, `I_(yy)`=M.I of the plan about y axis.

`=(pid^4)/64`

And V=volume of cylinder immersed

`=(pid^2)/4*h`

Thus,

`GM=d^2/(16h)-0.50503`

`=1^2/(16**0.9899)-0.50503`

`=-0.442`

Here the negative sign shows that the metacentre lies below the centre of gravity and hence the cylinder will be in unstable equilibrium and hence the cylinder will not float vertically in water.

Let T force is applied in a vertical chain attached at the centre of base of buoy to keep the buoy vertical.

Now, we have to find the combined position of c.g. and C.B. For combined centre of buoyancy, let h' be the depth of immersion when force T is applied.

From the law of floatation,

Total downward force = weight of water displaced

`7848+T=(pid^2)/4*rho_w*h'*g`

`7848+T=pi/4**1^2**1030**h'**9.81`

`h'=(7848+T)/7935.89`

Now the distance of new C.B is,

`C.B=AB=h'/2=(7848+T)/15871.8`

Now

Let,

`W_c`be the weight of cylinder

`x_1` be the distance of c.g (weight acting point) from A

`x_2` be the distance of application of T force from A.

Now, the combined c.g. due to weight of cylinder and due to tension T in the chain from A is,

`AG'=(W_c*x_1+T*x_2)/(W_c+T)`

`=((7848**2/2)+(T**0))/(7848+T)`

`=7848/(7848+T)`

Also,

`B'G'=AG' - AB'`

`=7848/(7848+T) - (7848+T)/15871.8`

Now the metacentric height is,

`GM=I/V-B'G'`

`=(pid^4)/(64**(pid^2)/4*h') -B'G'`

`=1/(16h')-B'G'`

`=1/(16 **(7848+T)/7935.89)-7848/(7848+T) +(7848+T)/15871.8`

Now for stable equilibrium,

`GM >=0`

`=1/(16 **(7848+T)/7935.89)-7848/(7848+T) +(7848+T)/15871.8 >=0`

`-117632/(16 (7848+T))+(7848+T)/(15871.8)>=0`

`(7848+T)/(15871.8)>= 117632/(16 (7848+T))`

`(7848+T)^2 >=(1080.23^2)`

`7848+T>=1080.23`

`T>=2954.3 N`

Thus the force in the chain must be at least equal to 2954.3 N so that the cylindrical buoy can be kept in vertical position.

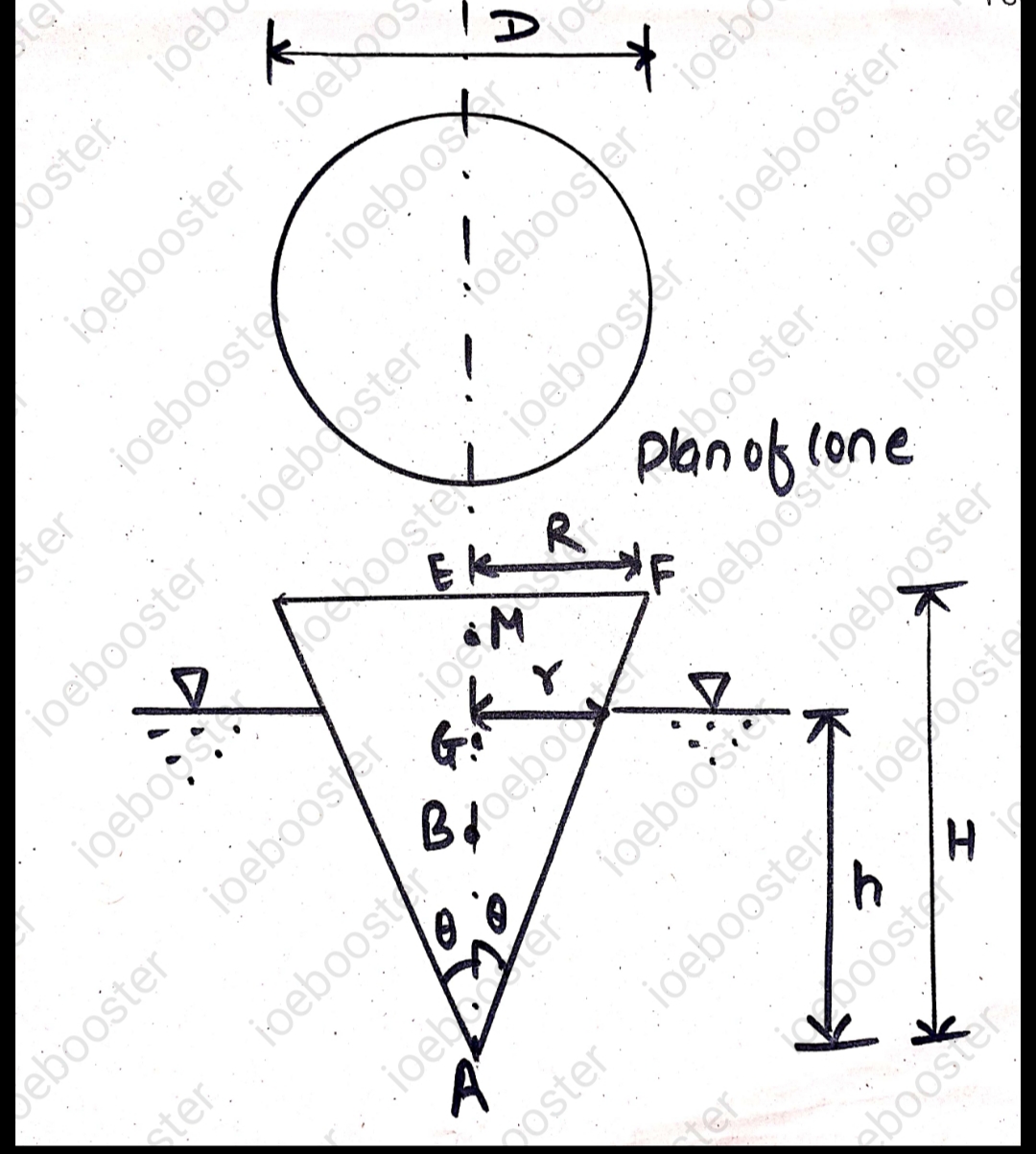
10. A solid cone floats in water with its apex downwards. Determine least apex angle of cone for stable equilibrium. The specific gravity of cone is 0.8.

A solid cone floats in water with its apex downwards. Determine the least apex angle of the cone for stable equilibrium. The specific gravity of the cone is 0.8.

SOLUTION:

Let,

D be the diameter of cone

d be the diameter of cone at water level

`2theta` be the apex angle of the cone

H be the height of cone

h be the depth of cone in water

G be the c.g. of the cone

B be the C.B. of the cone

We know that, for cone,

`AG=3/4H` and `AB=3/4h`

Also,

Volume of water displaced is,

`=1/3pir^2h`

And the volume of the cone is,

`=1/3piR^2H`

Thus the weight of the cone is,

`=800**9.81**1/3**piR^2H`

Now from `triangle AEF`,

`tantheta=R/H`

`R=H tantheta`

Similarly, `r=htantheta`

Thus the weight of cone is,

`=800g**1/3pi**(Htantheta)^2**H`

`=(800g**pi**H^3tan^2theta)/3`

Weight of water displaced is given as,

`=(1000g**pi**h^3tan^2theta)/3`

Now from the law of floatation,

Weight of cone = weight of water displaced

`(800g**pi**H^3tan^2theta)/3=(1000g**pi**h^3tan^2theta )/3`

`800H^3=100h^3`

`H/h=(10/8)^(�??)`

Also the metacentric height is,

`GM=I_(yy)/V-BG`

Where, `I_(yy)`=M.I of the plan at water line about y axis.

`=(pid^4)/64`

And V=volume of cone in water

`=1/3pir^2*h`

`=�??(pid^2h)/4`

And `BG=3/4 (H-h)`

Thus,

`GM=((pid^4)/64)/((pid^2h)/12)-3/4 (H-h)`

`=(12r^2)/(16h)-3/4(H-h)`

`=3/4htan^2theta-3/4 (H-h)`

For stability,

`GM >0`

`htan^2theta>H-h`

`1+tan^2theta>(10/8)^(�??)`

`theta>15^0 31'`

`2theta >31^0 3'`

Thus the minimum apex angle is `31^0 3'`.

All Chapters

View all Chapter and number of question available From each chapter from fluid-mechanics

Properties of fluid

properties of fluids
complete IOE solution on fluid mechanics
Detailed description chapterwise
Unlimited Numericals problem solved with updation daily
And much more

Hydrostatics

Hydrostatics basic theory
All important Numericals
IOE,PU, MIT,A.M.I.E,Delhi university,EUPS,Engineering service exam solved problems
Detailed explanation

Hydrostatics- Buoyancy and metacentric height

detailed explanation of force of buoyancy, metacentric height,stability of floating body
unlimited numericals solved with updation weekly
including IOE , PU, KU, GATE, MIT, ANNA UNIVERSITY,UPSC EXAM SOLUTIONS
And much more

ORIFICES AND WEIRS

Complete IOE and GATE EXAM SOLUTION along with numerous Numericals from Fluid mechanics

Topics

This Chapter hydrostatics-buoyancy-and-metacentric-height consists of the following topics

detailed explanation of force of buoyancy

metacentric height

stability of floating bodies

IOE

PU

KU

GATE

MIT

ANNA UNIVERSITY

UPSC EXAM SOLUTIONS

A wooden log of 0.6 m diameter and 5m in length is floating in river water. Find depth of wooden log in water when specific gravity of log is 0.7.

;

A metallic cube 30 cm side and weighing 450 N is lowered into a tank containing a two layer fluid of water and mercury. Determine position of block at mercury-water interface at equilibrium condition. [ANNA UNIVERSITY ]

;

A 8 cm side cube weighing 4N is immersed in a liquid of relative density 0.8 contained in a rectangular tank of cross sectional area 12 cm ** 12 cm. If tank contains liquid to a height of 6.4 cm before immersion, determine levels of bottom of cube and liquid surface.

;

The wooden beam shown in figure is 200 mm 200 mm 5 m long. It is hinged at A and remains in equilibrium at `ta` with horizontal. Find inclination `ta`. The specific gravity of wood can be taken as 0.70.

;

A wooden block of volume `0.03 m^3` weighing 210 N is attached to one end of a 3.5 m long wooden rod are under hinged to a wall. The block and part of rod are under water in position shown in figure. Find inclination `ta` of rod with horizontal. The rod weighs 15 N and has a uniform sectional area of 2000 `mm^2`.

;

Two spheres weighing 10 KN and 25 KN are each 1.6 m in diameter. They are connected by a short rope and placed in water. Find tension in connecting rope. Find also what portion of lighter sphere will protrude above water surface.

;

A body has cylindrical upper portion of 4m diameter and 2.4 m deep. The lower portion, which is curved; displaces a volume of 800 litres of water and its centre of buoyancy is situated 2.6m below top of cylinder. The centre of gravity of whole body is 1.6 m below top of cylinder and total displacement of water is 52 KN. Find metacentric height of body.

;

A hollow cylinder closed at both ends has an outside diameter of 1.25 m, length 3.5 m and specific weight 75 KN/`m^3`. If cylinder is to float just in stable equilibrium in sea water ( specific weight 10 KN/`m^3`), find its minimum permissible thickness.

;

Show that a cylindrical buoy of 1m diameter and 2m height weighing 7.848 KN will not float vertically in sea water of density 1030 kg/`m^3`. Find force necessary in a vertical chain attached at centre of base of buoy that will keep it vertical.

;

A solid cone floats in water with its apex downwards. Determine least apex angle of cone for stable equilibrium. The specific gravity of cone is 0.8.

;

Guest You need to login to ask any Questions from chapter hydrostatics-buoyancy-and-metacentric-height of fluid-mechanics

Chapter:

All Chapters

Dimensional Analysis, Similitude and Physical Modelling

Flow Past Through Submerged Body

Boundary Layer Theory

Properties of fluid

Hydrostatics

Hydrostatics- Buoyancy and metacentric height

ORIFICES AND WEIRS

Topics

detailed explanation of force of buoyancy

metacentric height

stability of floating bodies

IOE

PU

KU

GATE

MIT

ANNA UNIVERSITY

UPSC EXAM SOLUTIONS

A wooden log of 0.6 m diameter and 5m in length is floating in river water. Find depth of wooden log in water when specific gravity of log is 0.7.

A metallic cube 30 cm side and weighing 450 N is lowered into a tank containing a two layer fluid of water and mercury. Determine position of block at mercury-water interface at equilibrium condition. [ANNA UNIVERSITY ]

A 8 cm side cube weighing 4N is immersed in a liquid of relative density 0.8 contained in a rectangular tank of cross sectional area 12 cm ** 12 cm. If tank contains liquid to a height of 6.4 cm before immersion, determine levels of bottom of cube and liquid surface.

The wooden beam shown in figure is 200 mm ** 200 mm ** 5 m long. It is hinged at A and remains in equilibrium at `ta` with horizontal. Find inclination `ta`. The specific gravity of wood can be taken as 0.70.

Two spheres weighing 10 KN and 25 KN are each 1.6 m in diameter. They are connected by a short rope and placed in water. Find tension in connecting rope. Find also what portion of lighter sphere will protrude above water surface.

A hollow cylinder closed at both ends has an outside diameter of 1.25 m, length 3.5 m and specific weight 75 KN/`m^3`. If cylinder is to float just in stable equilibrium in sea water ( specific weight 10 KN/`m^3`), find its minimum permissible thickness.

Show that a cylindrical buoy of 1m diameter and 2m height weighing 7.848 KN will not float vertically in sea water of density 1030 kg/`m^3`. Find force necessary in a vertical chain attached at centre of base of buoy that will keep it vertical.

A solid cone floats in water with its apex downwards. Determine least apex angle of cone for stable equilibrium. The specific gravity of cone is 0.8.

Guest
You need to login to ask any Questions from chapter hydrostatics-buoyancy-and-metacentric-height of fluid-mechanics

The wooden beam shown in figure is 200 mm 200 mm 5 m long. It is hinged at A and remains in equilibrium at `ta` with horizontal. Find inclination `ta`. The specific gravity of wood can be taken as 0.70.