Chapter:
1. Define fluid.
A fluid is a substance that deforms continuously under the application of shear stress no matter how small the shear stress may be. A fluid may be classified as:
Liquid
Gas
Vapour
Ideal Fluids:
An ideal fluid is one which has no viscosity and surface tension and is incompressible. In true sense, no such fluid exists in nature. However fluids which have low viscosities such as water and air can be treated as ideal fluids under certain conditions.
Real Fluids:
A real practical fluid is one which has viscosity, surface tension and compressibility in addition to the density. The real fluids are actually available in nature.
2. Explain continuum concept of Fluid.
A continuous and homogeneous medium is called continuum. From the continuum view point, the overall properties and behaviour of fluids can be studied without regard for its atomic and molecular structure. A fluid behaves as if it were comprised of continuous matter that is infinitely divisible into smaller and smaller parts. This idea is called continuum assumption.
Thus, the fluid properties such as density, temperature, velocity and so on can be considered to be constant at any point and changes due to molecular motion may be ignored.
This assumption break down in case of rarefied gases, for which the mean free path of the molecules to the physical dimensions of the problem is larger.
3. Explain various properties of Fluids.
Properties of Fluids:
Density
Specific gravity
Viscosity
Vapour Pressure
Cohesion
Adhesion
Surface Tension
Capillarity
Compressibility
Density:
The density (also known as mass density or specific mass) of a liquid may be defined as the mass per unit volume at a standard temperature and pressure. It is usually denoted by `rho`.
`rho=M/V`
Its units are kg/`m^3`
Specific gravity:
Specific gravity is the ratio of the specific weight of the liquid to the specific weight of a standard fluid(air for gases and water for liquid). It is dimensionless and has no units. It is represented by S.
Viscosity:
Viscosity is defined as the property of the fluid by virtue of which it offers resistance to the movement of one layer of fluid over an adjacent layer. It is primarily due to cohesion and molecular momentum exchange between the fluid layers, and as flow occurs these effects appear as shearing stresses between the moving layers of fluid.
From Newton's law of viscosity,
`tau=mu*(du)/(dy)`
Where, `mu` is the dynamic viscosity.
Its SI unit is Ns/`m^2` and cgs unit is poise.
1 poise=` 1/10` Ns/`m^2`
Kinematic viscosity, `nu`,is defined as the ratio of dynamic viscosity and density of fluid.i.e,
`nu=mu/rho`
Its SI unit is `m^2/(sec)` and CGS unit is stoke.
1 stokes`= 10^(-4) m^2/(sec)`
Variation of viscosity with Temperature:
The viscosity of liquids decreases but that of gases increases with increase in temperature. This is due to the reason that in liquids the shear stress is due to the inter- molecular cohesion which decreases with increase of temperature. In gases the inter- molecular cohesion is negligible and the shear stress is due to exchange of momentum of the molecules, normal to the direction of motion. The molecular activity increases with rise in temperature and so the viscosity of gas also increases with temperature.
Cohesion:
Cohesion means intermolecular attraction between molecules of the same liquid. It enables a liquid to resist small amount of tensile stresses. Cohesion is a tendency of the liquid to remain as one assemblage of particles. �??Surface tension�?� is due to cohesion between particles at the free surface.
Adhesion:
Adhesion means attraction between the molecules of a liquid and the molecules of a solid boundary surface in contact with the liquid. This property enables a liquid to stick to another body.
Capillary action is due to both cohesion and adhesion.
Surface Tension:
Surface tension is defined as the tensile force acting on the surface of a liquid in contact with a gas or on the surface between two immiscible liquids such that the contact surface behaves like a membrane under tension.
For liquid droplets (say water bubble),
`P=(4*sigma)/d`
For hollow bubble (say soap bubble),
`P=(8*sigma)/d`
For liquid jet,
`P=(2*sigma)/d`
Where, `sigma`=surface tension
P= pressure intensity inside the droplet
d= diameter of the droplet
Capillarity:
Capillarity is a phenomenon by which a liquid (depending upon its specific gravity) rises into a thin glass tube above or below its general level. This phenomenon is due to the combined effect of cohesion and adhesion of liquid particles.
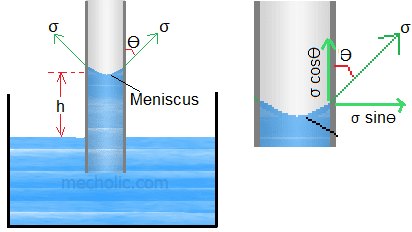
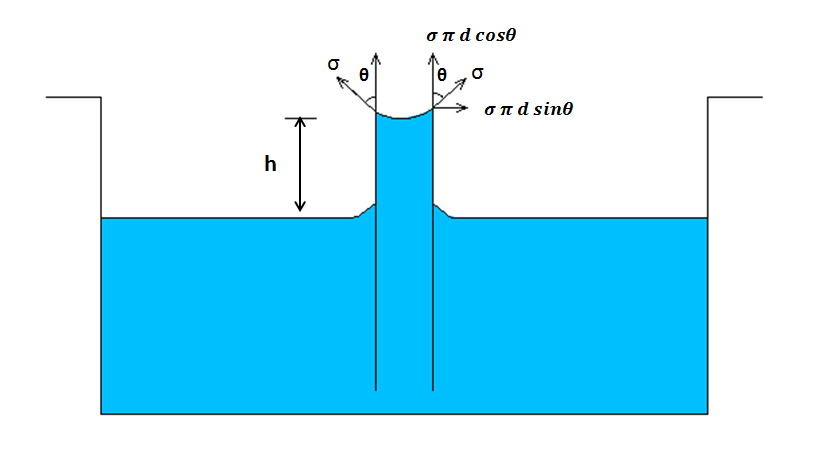
Expression for capillary rise:
Let us consider a glass tube of small diameter d opened at both ends and is inserted in a liquid, say water. The liquid will rise in the tube above the level of the liquid.
Let,
h= height of liquid in the tube
`sigma=`surface tension
d= diameter of the capillary tube
`theta=`angle of contact between the liquid and the tube
W= weight density
Now, the weight of the liquid inside the tube must be balanced by the vertical components of the surface tension force for equilibrium.
The weight of liquid of height h in the tube is given by,
`W=(pi*d^2)/4*h*rho*g`
Where, `rho` is the density of the liquid.
Also, the vertical component of the surface tension force is,
`=sigma*pi*d*cos theta`
At equilibrium, these forces must be equal and opposite. i.e,
`sigma*pi*d cos theta=(pi*d^2)/4*rho*g*h`
or, `h=(4 sigma cos theta)/(d rho g)`
or, `h=(r sigma cos theta)/(gamma*d)`
This is the expression for the capillary rise of liquid.
For water, `theta=0^0` so,
`h=(4*sigma)/(gamma*d)`
Similarly, we can obtain results for capillary fall (in case of mercury).
Vapour pressure:
The pressure at which the liquid and its vapour can exist in equilibrium at a certain temperature is termed as the Vapour Pressure of that liquid at that temperature.
Vapour Pressure of liquid increases with rise of temperature due to the increased molecular activity.
Cavitation:
The rapid vaporisation and recondensation of liquid as it flows through a region of low pressure is called cavitation.This phenomenon is not possible in gas because the gas doesnt changes it state at low pressure.
If at any point in flow, the local velocity is so high that the pressure in a liquid is reduced to its vapour pressure, the liquid will then vaporise at that point and bubbles of vapour will form. As a result of flow into a region of high pressure, the bubbles of vapour will suddenly condense i.e, collapse producing high dynamic pressure upon the adjacent solid walls.
Disadvantages of cavitation:
Turbine runners, pump impellers, and ship screw propellers are quickly damaged by cavitation phenomenon.
It may cause a drop in efficiency of a machine or propeller or other devices.
It increases the maintenance cost.
It produces undesirable noise and vibration.
4. Explain various methods for measurement of dynamic viscosity of a fluid.
Determination of Dynamic Viscosity:
Falling ball method
Rotating cylinder viscometer
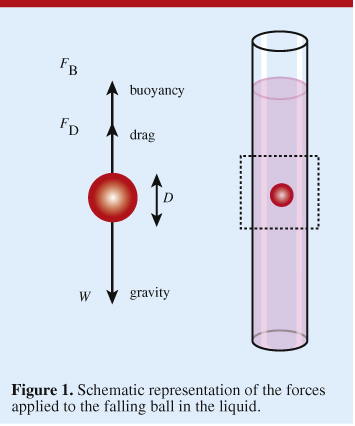
Falling ball method:
This method is used to measure viscosity by balancing the force..
If a body is dropped, starting from rest, in the atmosphere, it will accelerate due to gravity. As the speed of body increases, the body will experience a drag force, which tends to oppose the motion of the body. The drag force increases with a velocity of the fall and after certain time when velocity approaches terminal velocity, the upward drag would just balances the downward weight force such that the net force acting on the body will be zero.
Figure below shows the small rigid sphere of radius r and density `rho_s` falling freely from rest under the action of gravity through a liquid of density `rho_l` and viscosity `mu`. After certain time, it attains the equilibrium state.
Now, at equilibrium state,
Stokes had experimentally found that,
Drag force=`6pi mu r V_t`
Weight= upthrust+ drag force
`4/3pi*r^3*rho_s*g=4/3pi*r^3*rho_l*g+6pi mu r V_t`
Solving for `mu`, we get,
`mu=2/9*(r^2)/(V_t)*(rho_s-rho_l)g`
This equation can be used to calculate the dynamic viscosity of a sphere. This is valid for laminar flow with Reynolds number less that 0.1.
Rotating cylinder viscometer:
Rotating cylinder is used to measure viscosity by balancing the torque.
Rotational viscometers use the idea that the torque required to turn an object in a fluid is a function of the viscosity of that fluid. They measure the torque required to rotate a disk or bob in a fluid at a known speed.
Figure below shows the experimental setup. Let the outer cylinder is rotating with constant angular velocity `omega` whereas the inner cylinder is stationary and equipped with torque measuring devices. Let `r_1` and `r_2`be the radius of outer and inner cylinder respectively. Let t be the thickness of fluid separating two cylinders.
Now, thickness of oil film is,`t=(r_1-r_2)`
The shear stress is,
`tau=mu*(du)/(dy)=mu*(2 pi*N*r_1)/(60t)`
Where, N is the revolution per minute of outer cylinder.
Now, viscous force is, `F=tau*A=mu*(2 pi*N*r_1)/(60t)*2pi*r_2*L`
Where, L is the length of cylinder.
Thus, the viscous torque is given by,
`T=F*r_2=mu*(2 pi*N*r_1)/(60t)*2pi*r_2*L*r_2`
or,`T=1/15*mu*(pi)^2*r_1*(r_2)^2*L*N`
or,`mu=(15t)/((pi)^2*r_1*(r_2)^2*L*N)`
This equation can be used to calculate the dynamic viscosity.
5. Explain compressibility of Fluids.
Compressibility is a measure of change in the volume of fluid under the effect of force/pressure or stress.
When fluid is acted upon by force, volume gets reduced. This effect is also judge by 'Bulk Modulus of elasticity'. The Compressibility coefficient can also be expressed as reciprocal of Bulk Modulus of elasticity.
Thus, - (Change in Volume/Original Volume = Change in Pressure/Bulk Modulus) as given by Equation (1).
The negative (-ve) sign suggests the volume gets decreased when pressure increases. When we consider the unit mass of fluid, Volume is reciprocal of density (as given by Equation (2)). Now by differentiating the and substituting the value of V and dV, final equation is equation (3) which gives relation between change in pressure and change in density of fluid and also density also affected by temperature change. Thus during compression, rise in temperature causes the change in density as well as change in pressure.
For a given mass of fluid,
`m=rho*V`
Differentiating throughout, we get,
`dm=rho*dv+V*drho`
Since mass is constant, dm=0,
or, `0=rho*dv+V*drho`
or, `-(dV)/V=(drho)/(rho)`.... (i)
We know that, the bulk modulus of elasticity is,
`K=1/(beta)`
Where, `beta` is the compressibility of Fluids
or, `K=-(dp)/((dV)/V)`... (ii)
From (i) and (ii),
`K=rho*(dP)/(drho)`
6. Suppose water rise predicted by capillarity formula exceeds height of capillary tube. Does water overflow? Explain with mamatical expression.
We know that Capillary action occurs when the force of adhesion between molecules of liquid and walls of a capillary tube (container) is stronger than the force of cohesion between molecules of a liquid. Due to this the liquid has the ability to flow in narrow spaces, or even against gravity.
The height
h of a liquid column is given as
`h=(4 sigma cos theta)/(rho g d)`
where
`sigma` is the liquid-air surface tension.
`theta` is angle of contact,
`rho` is the density of liquid,
`g` is acceleration due to gravity, and
`d` is the diameter of capillary tube.
When length of tube is less than the height of capillary rise, the liquid molecules on reaching top of the capillary come into contact with horizontal surface of the tube. The surface tension becomes horizontal. There is no vertical force to pull the liquid up and it stops rising.
Also at each point at the capillary edge there exits a point diametrically opposite at which the surface tension is equal and opposite.
Thus an equilibrium is established, and the liquid does not spill over.
7. The general relation between shear stress and velocity gradient of fluid can be written as:
`tau=A ((du)/(dy))^n+B`
Where A , B and n are constants that depend upon type of fluid and condition imposed on flow. Comment value of se constants so that fluid may behave as:
- An ideal fluid
- A newtonian fluid
- A non newtonian fluid
Also indicate wher fluid with following characteristics is Newtonian or non-Newtonian.
- `tau=A*y+B` and `U=C_1+C_2*y+C_3*y^2`
- `tau=A*y^(n (n-1))` and `U=C*y^n`
Solution:
Given,
`tau=A ((du)/(dy))^n+B`
IDEAL FLUID:
Since an ideal fluid has zero viscosity (i.e, shear stress is always zero regardless of the motion of the fluid), we have,
`A=B=0`
A NEWTONIAN FLUID:
Since a newtonian fluid follows the newtons law of viscosity, `tau=mu*(du)/(dy)`, therefore compairing, we get,
`n=1`,
`A=mu`,
`B=0`
Air,water,kerosine etc behaves as Newtonian fluid under normal working conditions.
A NON-NEWTONIAN FLUID:
Depending upon the value of power index `n`, the non-Newtonian fluid are classified as:
If `n>1` and B=0, Dilatent fluid. Example: sugar solution, aqueous suspension and printing ink.
If `n<1` and B=0, Pseudo-plastic fluid. Example: Blood, milk, liquid cement and clay.
If `n=1` and `B=tau_0`, then Bingham fluid or ideal plastic. Example: sewage sludge, water suspension of clay and flyash.
Case II:
Again, given,
`tau=A*y+B` and `U=C_1+C_2*y+C_3*y^2`
Now,
`(du)/(dy)=C_2+2*C_3y`
For Newtonian fluid,
`tau=mu*(du)/(dy)`
Thus, `tau=mu*(C_2+2*C_3y)=2muC_3y+muC_2`
Since this has the same form as given shear stress, therefore the fluid characteristics corresponds to that of an Newtonian fluid.
Case III:
Given,
`tau=A*y^(n (n-1))` and `U=C*y^n`
Now,
`(du)/(dy)=c*n*y^(n-1)`
For a Newtonian fluid,
`tau=mu*(du)/(dy)=mu(cny^(n-1))`
Or, `tau=mu*c*n*y^(n-1)`
This expression does not confirms to the value of shear stress and hence this fluid is non-Newtonian in character.
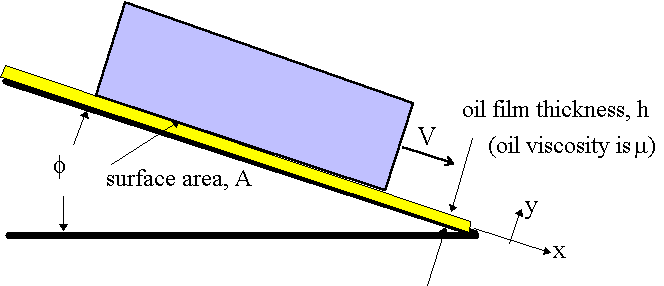
8. A plate having an area of `0.6 m^2` is sliding down inclined plane at an angle of `30^0` to horizontal with a velocity of 0.36 m/sec. There is a cushion of fluid 1.8 mm thick between plane and plate. Find viscosity of fluid if weight of plate is 280N.
SOLUTION:
Given,
Area of plate,`A=0.6 m^2`
Velocity of the plate,`u=0.36`m/s
Thickness of the film,`dy=1.8`mm
Weight of the plate,` W=280 N`
Viscosity of the fluid,` mu=?`
Now,
Shear force on the bottom surface of the plate is given by,
F= component of weight along the plane.
or, `F=W*sin30 =140 N`
Thus, shear stress `tau=F/A=140/0.6 =233.33` N/`m^2`
We have,
`tau=mu*(du)/(dy)`
or, `mu=233.33/0.36 *1.8/1000=1.1667`Ns/`m^2`
or, `mu=11.667` poise.
9. The space between two square flat parallel plate is filled with oil. Each side of plate os 720 mm. The thickness of oil film is 15 mm. The upper plate which moves at 3 m/s requires a force of 120 N to maintain speed. Determine:
- dynamic viscosity of oil
- kinematic viscosity of oil if specific gravity of oil is 0.95
SOLUTION:
Given,
Each side of the square plate =720 mm = 0.72 m
Thickness of the oil film, `dy=15 mm=0.015 m`
Velocity of the upper plate, `du=3`m/s.
Force required on the upper plate; `F=120 N`
Dynamic viscosity, `mu=?`
Kinematic viscosity, `nu=?`
Now,we have,
`tau=mu*(du)/(dy)`
or, `mu=tau*(dy)/(du)`
`=F/A*(dy)/(du)`
`=120/(0.72\ *\ 0.72)*0.015/3`
Thus, `mu=1.16`Ns/`m^2` `=11.6`poise.
Also, we have,
Kinematic viscosity, `nu=mu/rho`
Also, specific gravity`=0.95=rho/1000`
Thus, `rho=950`kg/`m^3`
Thus,
`nu=1.16/950`$*$1.22$ *$`10^(-3) m^2/s`
`nu=12.21` stokes.
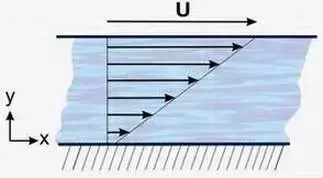
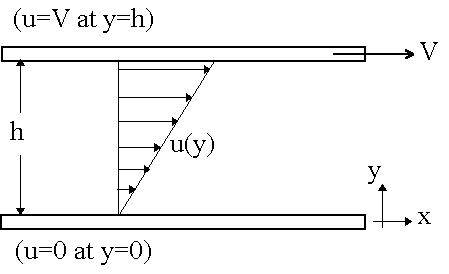
10. A lubricating oil of viscosity `mu` undergoes steady shear between a fixed lower plate and an upper plate moving at speed V. The clearance between plate is h. Show that linear velocity profile results if fluid doesn't slip at eir place.
SOLUTION:
For the given geometry and motion, the shear stress `tau` is constant throughout.
Now, from Newton's law of viscosity, We have,
`tau=mu*(du)/(dy)`, where shear stress is constant.
or, `(du)/(dy)=tau/mu=Constant`
or, `u=a+by`
The constant a and b are evaluated from no slip conditions at the upper and the lower plates.
So, at y=0, u=0
Thus, a=0
Also,
At y=h, u=V,
`V=a+bh`
or,`V=0+bh`
or, `b=V/h`
Thus, the velocity profile between the plates is given by,
`u=V/h*y`, and is linear as shown in the figure.
All Chapters
Dimensional Analysis, Similitude and Physical Modelling
Flow Past Through Submerged Body
Boundary Layer Theory
Properties of fluid
- properties of fluids
- complete IOE solution on fluid mechanics
- Detailed description chapterwise
- Unlimited Numericals problem solved with updation daily
- And much more
Hydrostatics
- Hydrostatics basic theory
- All important Numericals
- IOE,PU, MIT,A.M.I.E,Delhi university,EUPS,Engineering service exam solved problems
- Detailed explanation
Hydrostatics- Buoyancy and metacentric height
- detailed explanation of force of buoyancy, metacentric height,stability of floating body
- unlimited numericals solved with updation weekly
- including IOE , PU, KU, GATE, MIT, ANNA UNIVERSITY,UPSC EXAM SOLUTIONS
- And much more
 Guest
Guest