Chapter:
1. Vena contracta:
Vena contracta is the point in a fluid stream where the diameter of the stream is the least, and fluid velocity is at its maximum.
How is vena contracta formed in fluid flow?
The reason for the phenomenon Vena contracta is that the fluid streamline cannot abruptly changes direction† and they are unable to closely follow the sharp angles in orifices, nozzles and pipes. When fluid passes through the orifices, the gradual contraction of fluid takes place. The fluid stream begins to converge and passes through orifice.† The streamline continues to converging in smooth path even after it passes through the orifices. Fluid converges to the minimum section in downstream of flow and then it diverges again. This minimum cross section is known as vena contracta.
Types of orifices:
Orifice is defined as the small opening on side or bottom of a tank through which any kind of fluid is flowing.
Orifices are classified into small orifice and large orifice depending upon the size of orifice and head of fluid in that orifice.
†Small orifice is the one in which has the head of fluid from the centre of orifice is more than five times the depth of orifice.†
Also, the large orifice is the one which has the head is less than five times the depth of orifice.
Based on shape of orifice they are classified as following:
Rectangular orifice
Circular orifice
Triangular orifice
Square orifice
Hydraulic Co-efficients
There are mainly 3 hydraulic coefficients, they are as follows:
Co efficient of contraction, Cc
Coefficient of discharge, Cd
Coefficient of velocity, Cv
Coefficient of Contraction (Cc)
It is the ratio of area of water jet at vena-contracta to the area of the orifice.
`C_c=a_c/a`
Where,
`a_c` = Area of jet at vena-contracta
a = Area of the orifice
Coefficient of Velocity (Cv)
It is the ratio of velocity of water jet at vena-contracta to the theoretical velocity.
Coefficient of discharge (Cd)
It is the ratio of actual discharge to the theoretical discharge.
The relation between the coefficient of contraction, coefficient of velocity and coefficient of discharge can be expressed as,
`C_d=C_c*C_v`
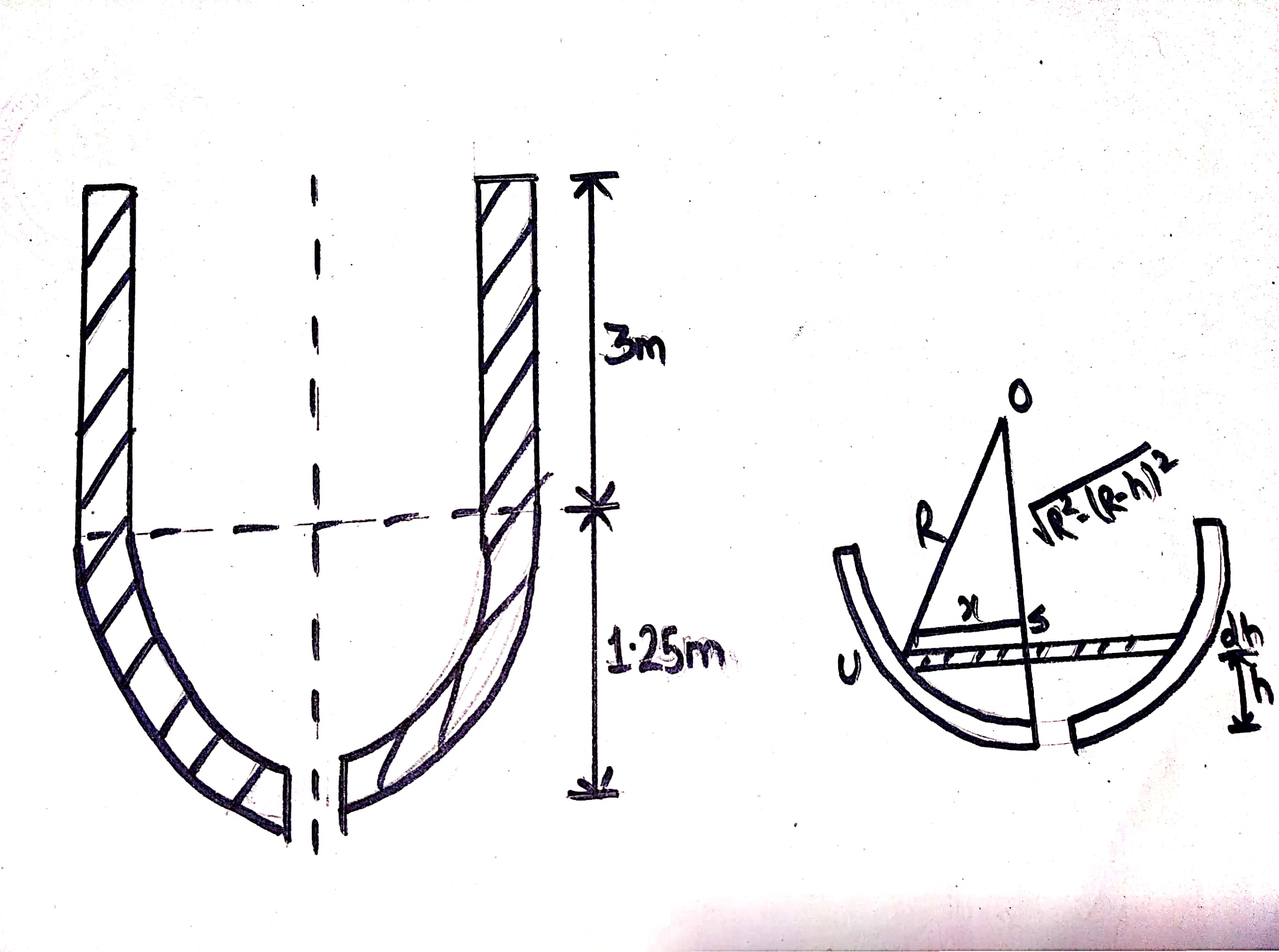
2. A 600 mm diameter vertical tank contains water to a depth of 2.5m. There are two orifices in tank. One at bottom and or in one of vertical sides of tank at a height of 1.5m above bottom. If area of each of orifice is ` 12 cm^2` and`C_d=0.6`, Calculate time required to empty tank.
SOLUTION:
Here, the area of the cylindrical tank is,
`A=pi/4**0.6^2=0.2827 m^2`
And, the area of the orifice is,`a=0.0012 m^2`
Let,
`T_1` be the time required to bring water level from AB to CD.
`T_2` be the time to empty the water below the portion CD
Thus the total time to empty the tank is,
`T=T_1+T_2`... (i)
Initially, let us consider an instant such that the height of water above the centre of upper orifice is h m. Let us say that during time `dT`, the level of water fall by`dh`.
Now from the principle of continuity, 
`-A*dh=(Q_1+Q_2)dT`
`-A*dh=C_d*a*root ()(2g)*(root ()(h)+root ()(h+1.5))`
`dT=-A/(C_d*a*root ()(2g))*(dh)/(root ()(h)+root ()(h+1.5))`
The total time required to drop level of water from AB to CD can be obtained by integrating this equation from limit h=1 to h=0 since h is assumed to be a  depth of water surface above upper orifice.
`T_1=-A/(C_d*a*root ()(2g))int_{1}^{0}(dh)/(root ()(h)+root ()(h+1.5))`
`=-A/(C_d*a*root ()(2g))int_{1}^{0} (root ()(h)-root ()(h+1.5))/(-1.5)dh`
Solving this using calculator,we get,
`T_1=43.96 sec`
Again, let us assume that the water is at any height h above the bottom orifice at any instant of time t and let the level of water falls by an amount dh in small time interval dT.
Now from the principle of continuity, 
`-A*dh=C_d*a*root ()(2gh)*dT`
The total time required to drop level of water from CD to EF (i.e, empty tank) can be obtained by integrating this equation from limit h=1.5 to h=0 since h is assumed to be a  depth of water surface above lower orifice i.e,bottom of tank.
`T_2=-A/(C_d*a*root ()(2g)) int_{1.5}^{0}1/root ()(h)dh`
Solving this using calculator, we get,
`T_2=217.12 sec`
Thus the total time required to completely emptying the tank is,
`T=T_1+T_1`
`T=261.08 sec`
3. A tank has an upper cylindrical portion of 1.25 m radius and 3 m height with hemispherical base. The tank is provided with an orifice of 150 mm diameter at its bottom. Find time required to empty it if it is initially full of water.Take Cd =0.62 for orifice.
SOLUTION:
Radius of the tank, R = 1.25 m
Area of cylinder,`A=pi**1.25^2=4.908 m^2`
Area of orifice,`a=pi**0.15^2/4=0.01767 m^2`
Let,
`T_1` be the time required to empty the cylindrical portion .
`T_2` be the time to empty the hemispherical portion 
Thus the total time to empty the tank is,
`T=T_1+T_2`... (i)
Initially, let us consider an instant such that the height of water above the centre of orifice is h m. Let us say that during time `dT`, the level of water fall by`dh`.
Now from the principle of continuity, 
`-A*dh=C_d*a*root ()(2gh)*dT`
The total time required to empty the cylindrical  tank can be obtained by integrating this equation from limit h=1.25+3=4.25 to h=1.25 since h is assumed to be a  depth of water surface above the orifice i.e,bottom of tank.
`T_1=-A/(C_d*a*root ()(2g))\int_{4.25}^{1.25}root ()(h)dh`
Solving this using calculator, we get,
`T_1=190.85 sec`
Again, let us assume that the water is at any height h above the bottom orifice at any instant of time t and let the level of water falls by an amount dh in small time interval dT. Let x be the radius of the liquid surface.
Area of liquid surface is,`A=pix^2`
Now from the principle of continuity, 
`-A*dh=C_d*a*root ()(2gh)*dT`
`dT=-(pix^2 *dh)/(C_d*a*root ()(2gh))`
From figure,
`US=x=root ()(R^2-(R-h)^2)`
or,`x^2=2Rh-h^2`
Now,
The total time required to empty the hemispherical tank can be obtained by integrating this equation from limit h=1.25 to h=0 since h is assumed to be a  depth of water surface above the orifice i.e,bottom of tank.
`T_2=-pi/(C_d*a*root ()(2g))*\int_{1.5}^{0} (2Rh-h^2)/root ()(h)dh`
Solving this using calculator, we get,
`T_2=105.6 sec`
Thus the total time required to completely emptying the tank is,
`T=T_1+T_1=190.85+105.6`
`T=261.08 sec`
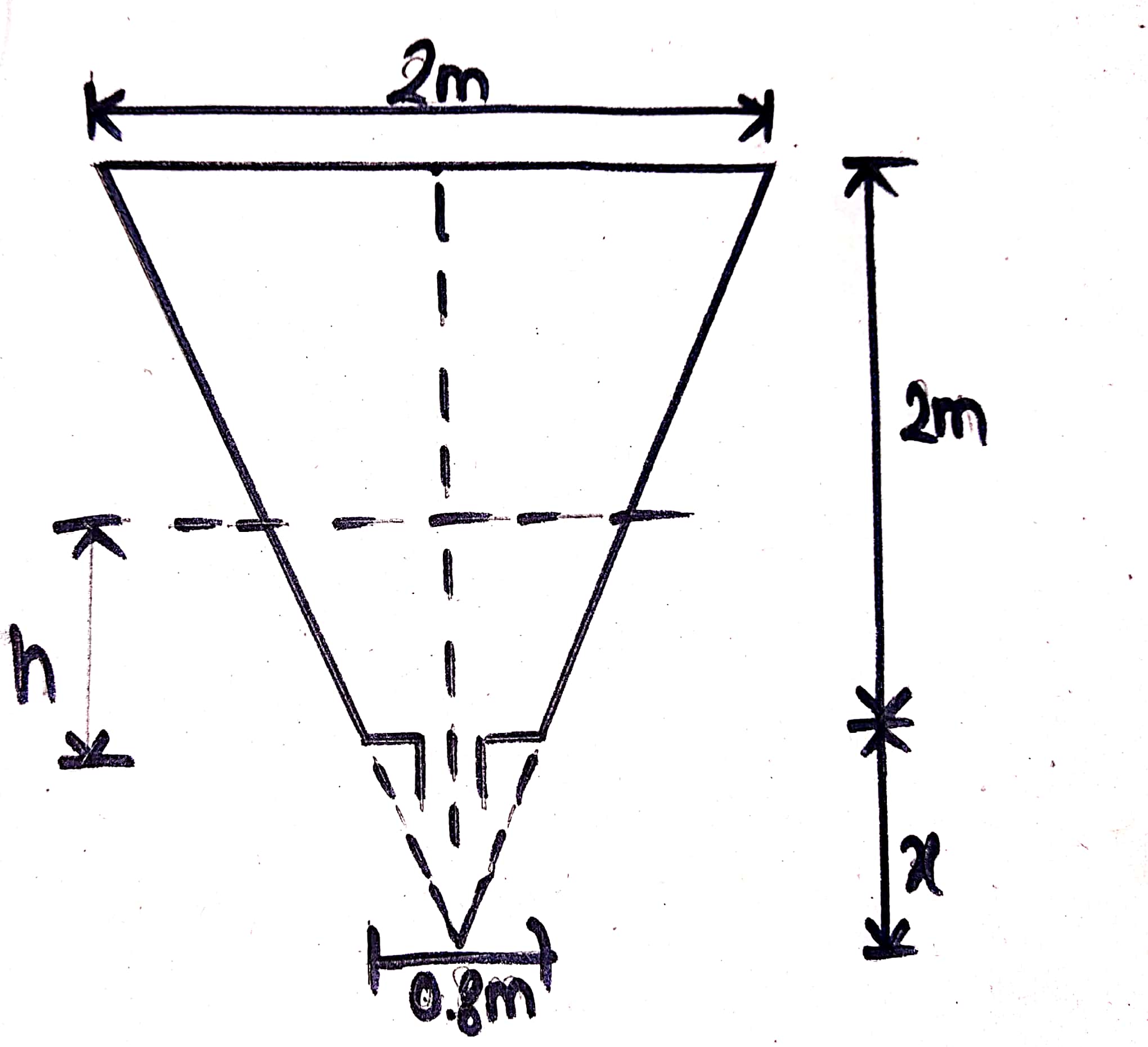
4. A tank is in form of a frustum of a cone having top diameter 2m, bottom diameter 0.8 m and height 2m and is full of water. Find time of emptying tank through orifice 100 mm in diameter at bottom. Take `C_d` as 0.625.
SOLUTION:
Here,
Area of orifice,`a=(pi**0.1^2)/4=0.0025pi \ m^2`
 Let us consider  any instant such that the height of water above the centre of orifice is h m. Let us say that during time `dT`, the level of water fall by`dh`. Let r be the radius of the liquid surface.
Now from the principle of continuity, 
`-A*dh=C_d*a*root ()(2gh)*dT`
`-pir^2dh=C_d*a*root ()(2gh)*dT`... (i)
Now from figure,
`0.4/x=1/(2+x)`
or,`0.8+0.4x=x`
`x=4/3`
Also,
`R/r=(2+x)/(x+h)`
`1/r=(10/3)/((4+3h)/3)`
`r=(4+3h)/10`
Now from equation  (i),
`-pi(4+3h)^2/100 dh=C_d*a*root ()(2gh)*dT`
`dT=-pi/(100C_d*a*root ()(2g))*((4+3h)^2)/(root ()(h))dh`
The total time required to empty the given tank can be obtained by integrating this equation from limit h=2 to h=0 since h is assumed to be a  depth of water surface above the orifice i.e,bottom of tank.
`T=-pi/(100C_d*a*root ()(2g))\int_{2}^{0}((4+3h)^2)/(root ()(h))dh `
Solving this using calculator, we get, 
`T=160.211 Sec`
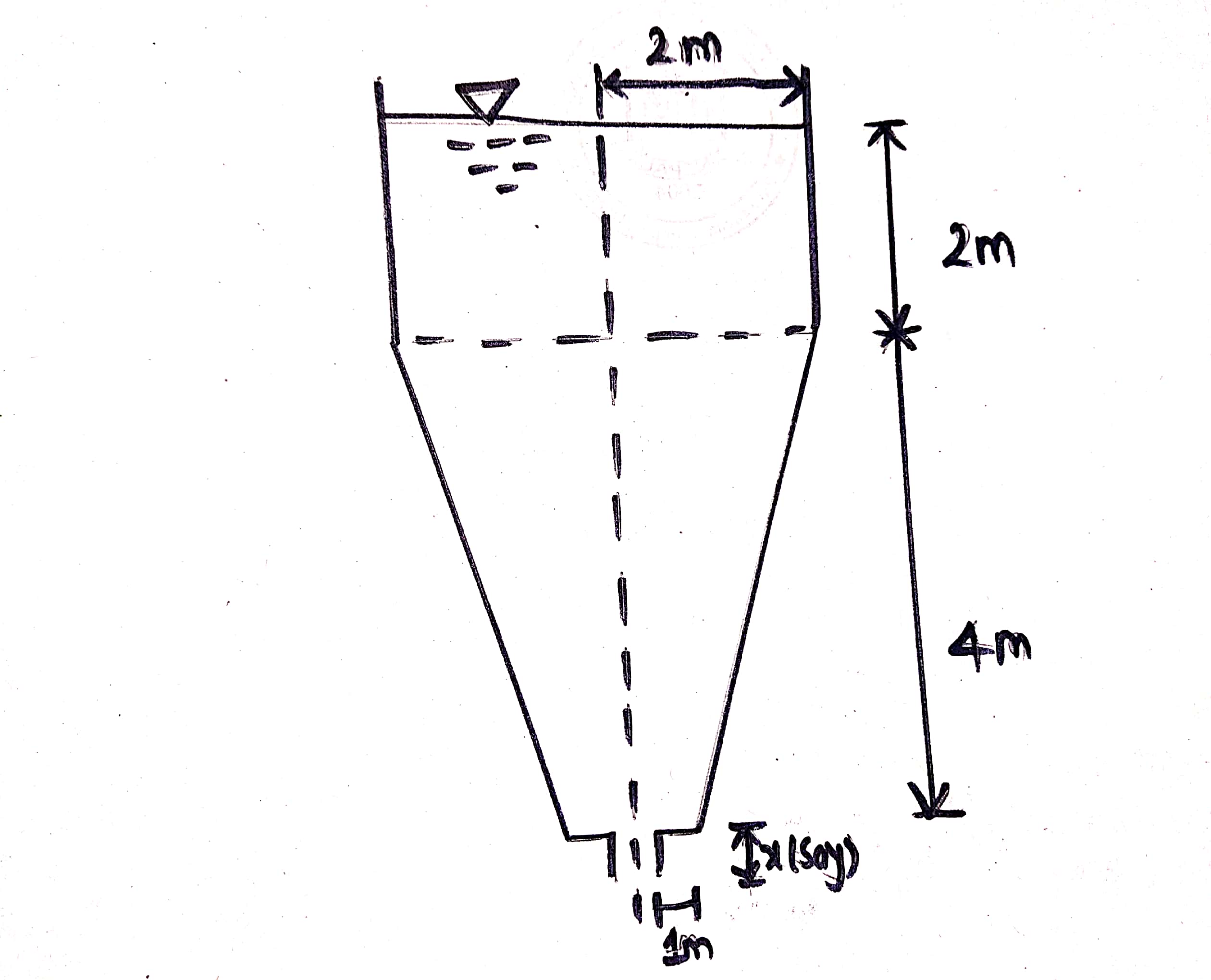
5. Find time of emptying of cylindrical vessel attached with conical vessel through a orifices of diameter 10 cm at bottom as shown in figure below. There is no inflow into tank. Take `C_d` as 0.6.
SOLUTION:
Here,
Area of orifice,`a=(pi**0.1^2)/4=0.00785\ m^2`
Area of cylindrical portion,`A=pi**2^2=12.57 m^2`
Let,
`T_1` be the time required to empty the cylindrical portion .
`T_2` be the time to empty the hemispherical portion 
Thus the total time to empty the tank is,
`T=T_1+T_2`... (i)
Initially, let us consider an instant such that the height of water above the centre of orifice is h m. Let us say that during time `dT`, the level of water fall by`dh`.
Now from the principle of continuity, 
`-A*dh=C_d*a*root ()(2gh)*dT`
The total time required to empty the cylindrical  tank can be obtained by integrating this equation from limit h=14+2=4.25 to h=4 since h is assumed to be a  depth of water surface above the orifice i.e,bottom of tank.
`T_1=-A/(C_d*a*root ()(2g))\int_{6}^{4}root ()(h)dh`
Solving this using calculator, we get,
`T_1=541.65 sec`
Again, let us assume that the water is at any height h above the bottom orifice at any instant of time t and let the level of water falls by an amount dh in small time interval dT. Let r be the radius of the conical liquid surface.
Now from the principle of continuity, 
`-A*dh=C_d*a*root ()(2gh)*dT`
`-pir^2dh=C_d*a*root ()(2gh)*dT`...(i)
Now from figure,
`1/x=2/(4+x)`
or,`x+4=2x`
`x=4`
Also,
`1/r=4/(x+h)`
`4r=h+4`
`r=(h+4)/4`
Now from equation  (i),
`-pi(h+4)^2/16 dh=C_d*a*root ()(2gh)*dT`
`dT=-pi/(16C_d*a*root ()(2g))*((4+h)^2)/(root ()(h))dh`
The total time required to empty the given tank can be obtained by integrating this equation from limit h=4 to h=0 since h is assumed to be a  depth of water surface above the orifice i.e,bottom of tank.
`T=-pi/(16C_d*a*root ()(2g))\int_{4}^{0}((4+h)^2)/(root ()(h))dh `
`T=-pi/(16C_d*a*root ()(2g))\int_{4}^{0}(h^(3/2)+8h^(1/2)+16h^(-1/2))`
`T=1124.42 Sec`
Thus the total time required to completely emptying the tank is,
`T=T_1+T_1=541.65+1124.42`
`T=1666.07 sec`
6. A swimming pool 30m long and 10m wide has a vertical sides and bottom at slope. The depth of water at shallow and deep sides are 2m and 5m respectively. Two outlets, each 0.4m diameter have been provided at each of deep and shallow ends. Calculate time taken to empty pool if both outlets are open. Take `C_d` as 0.6 for both openings.
SOLUTION:
Here,
Area of orifice,`a=(pi**0.4^2)/4=0.1256\ m^2`
Area of pool,`A=31**10=300 m^2`
Let,
`T_1` be the time required to bring water level from AB to CD.
`T_2` be the time to empty the water below the portion CD
Thus the total time to empty the tank is,
`T=T_1+T_2`... (i)
Initially, let us consider an instant such that the height of water above the centre of upper orifice is h m. Let us say that during time `dT`, the level of water fall by`dh`.
Now from the principle of continuity, 
`-A*dh=(Q_1+Q_2)dT`
`-A*dh=C_d*a*root ()(2g)*(root ()(h)+root ()(h+3))`
`dT=-A/(C_d*a*root ()(2g))*(dh)/(root ()(h)+root ()(h+3))`
The total time required to drop level of water from AB to CD can be obtained by integrating this equation from limit h=2 to h=0 since h is assumed to be a  depth of water surface above upper orifice.
`T_1=-A/(C_d*a*root ()(2g))\int_{2}^{0}(dh)/(root ()(h)+root ()(h+3))`
`=-A/(C_d*a*root ()(2g))\int_{2}^{0} (root ()(h)-root ()(h+3))/(-3)dh`
Solving this using calculator,we get,
`T_1=630.3 sec`
Again, let us assume that the water is at any height h above the bottom orifice at any instant of time t within the triangular element and let the level of water falls by an amount dh in small time interval dT.
Width of water surface is,
`=h/3**10`
And the area of water surface is,
`A=(h/3**10)**30=100h`
Now from the principle of continuity, 
`-A*dh=C_d*a*root ()(2gh)*dT`
The total time required to drop level of water from CD to E (i.e, empty tank) can be obtained by integrating this equation from limit h=3 to h=0 since h is assumed to be a  depth of water surface above lower orifice i.e,bottom of tank.
`T_2=-A/(C_d*a*root ()(2g))\int_{3}^{0}1/(root ()(h))dh`
`=-100/(C_d*a*root ()(2g))\int_{3}^{0}root ()(h)dh`
Solving this using calculator, we get,
`T_2=1037.7 sec`
Thus the total time required to completely emptying the tank is,
`T=T_1+T_1`
`T=630.3+1037.7`
`T=1668 sec`
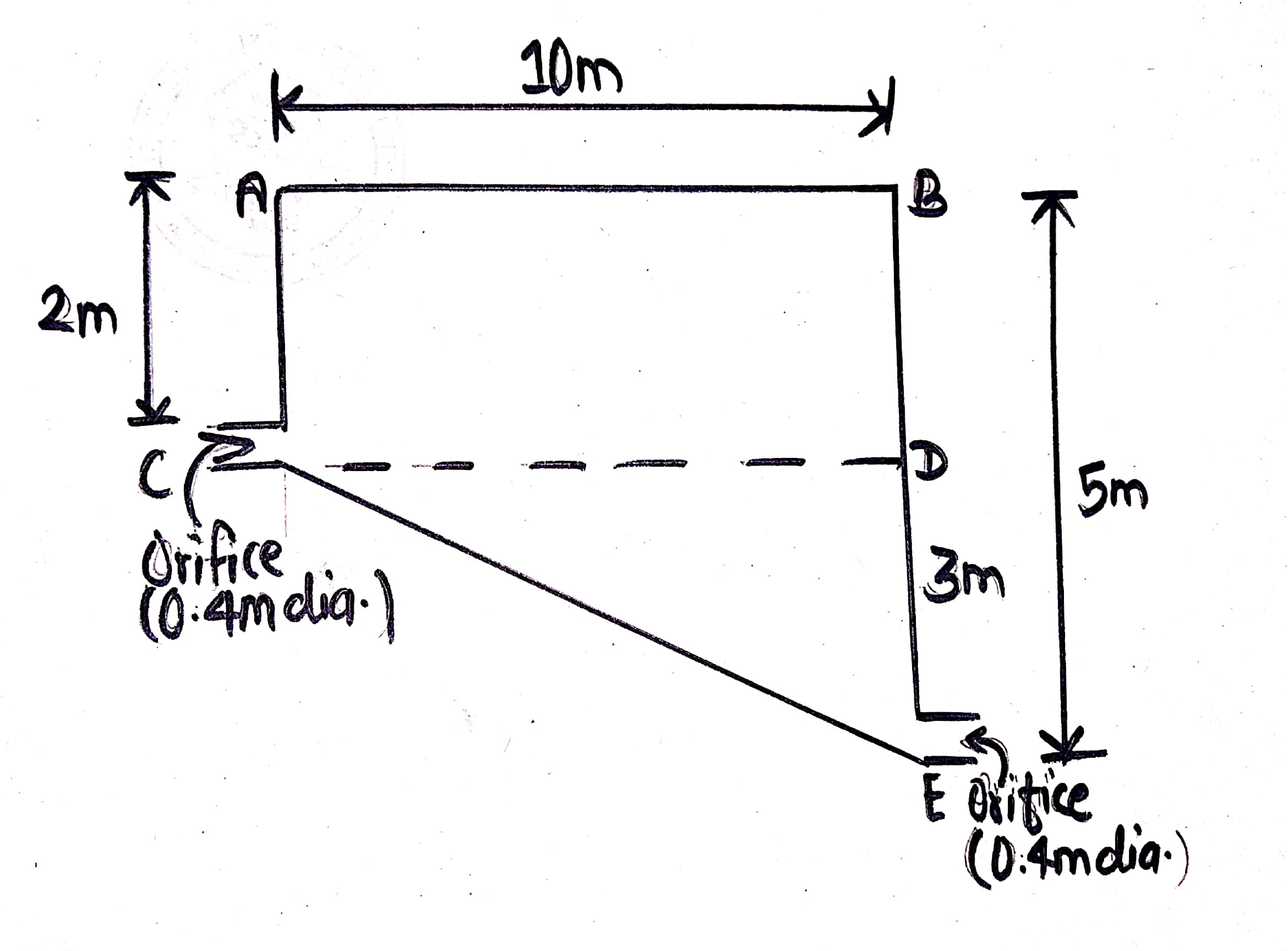
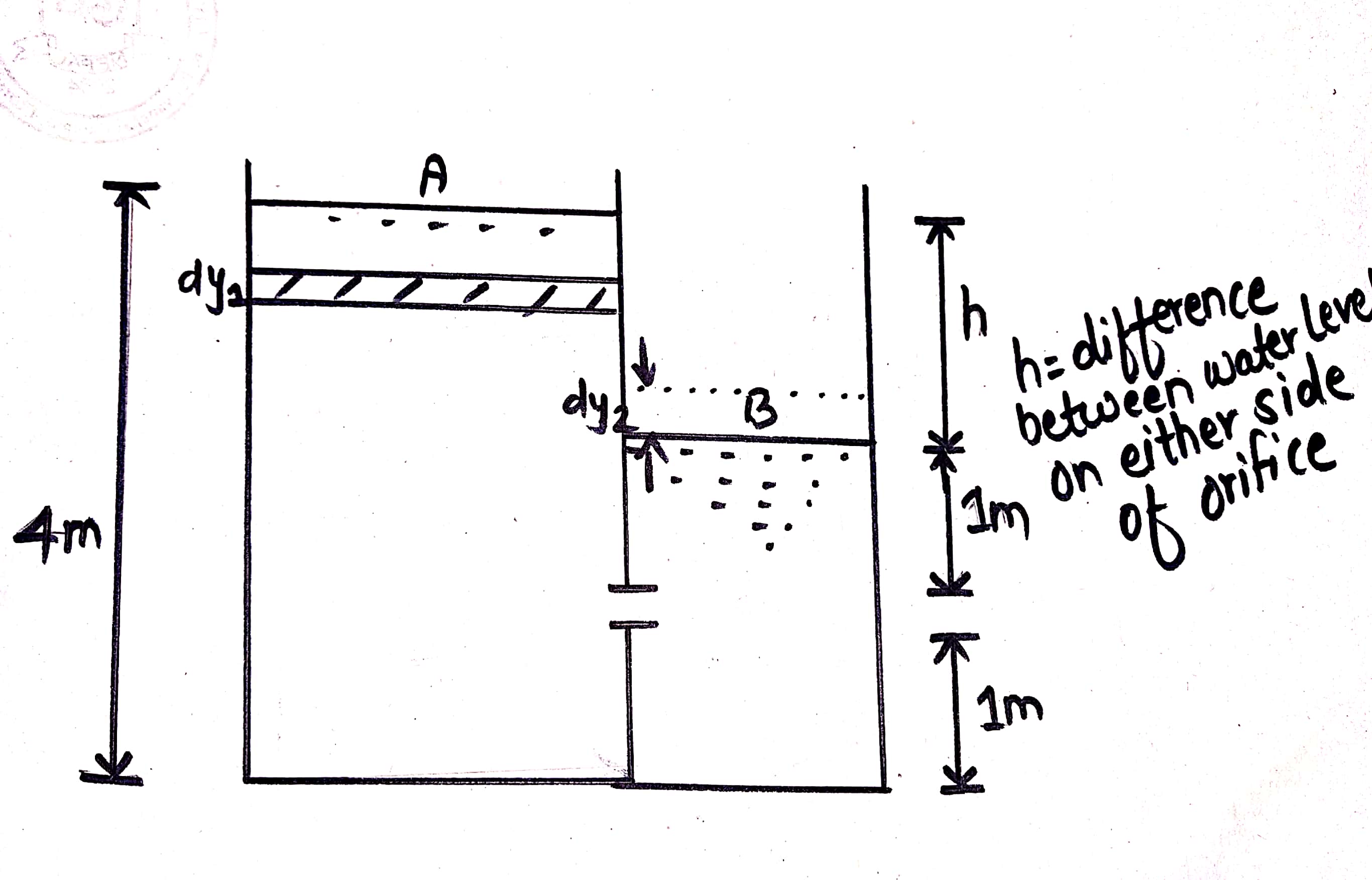
7. A vessel has compartments A and B communicating by an orifice `250 cm^2`, its centre being 1m above bottom of vessel. The cross section of A and B are `10 m^2` and `20m^2`. At certain time, water stands 4m in A and 2m in B. How soon reafter water will attain common level.
SOLUTION:
Here,
Area of orifice,`a=150 **10^(-4) m^2`
Area,`A_1=10 m^2`
Area,`A_2=20 m^2`
Let, 
h be the difference between water level on either side of the profile.
y be the depth of water in A at any instant.
dy be the change in depth of A during the small time interval dT.
Now, decrease in volume of water in A is,
`=A_1*dy=-10dy`
Similarly increase in volume of water in B is,
`=A_2*dy_2=20dy_2`
Since the decrease in volume of A corresponds to the increase in volume of B,
`dy_2=10/20*dy=1/2*dy`
Now the total change in level of water in small time dt is,
`dh=dy-(-dy_2)=3/2dy`
`dy=2/3dh`
Discharge through orifice in time dT is,
`=C_d*a*root ()(2gh) dT`.... (i)
Thus the decrease in volume of water in time dT is,
`=A_1*dy`
`=20**2/3dh`... (ii)
Thus from (i) and (ii),
`-10**2/3**dh=C_d*a*root ()(2gh) dT`
or,`\int_{0}^{T}dT=-20/(3**C_d**a**root ()(2g))*\int_{h}^{0} h^(-1/2) dh`
or,`T=20/(3**0.62**150**10^(-4)**root ()(2g))*2root ()(h)` ,where h=2
`T=457.7 Sec`
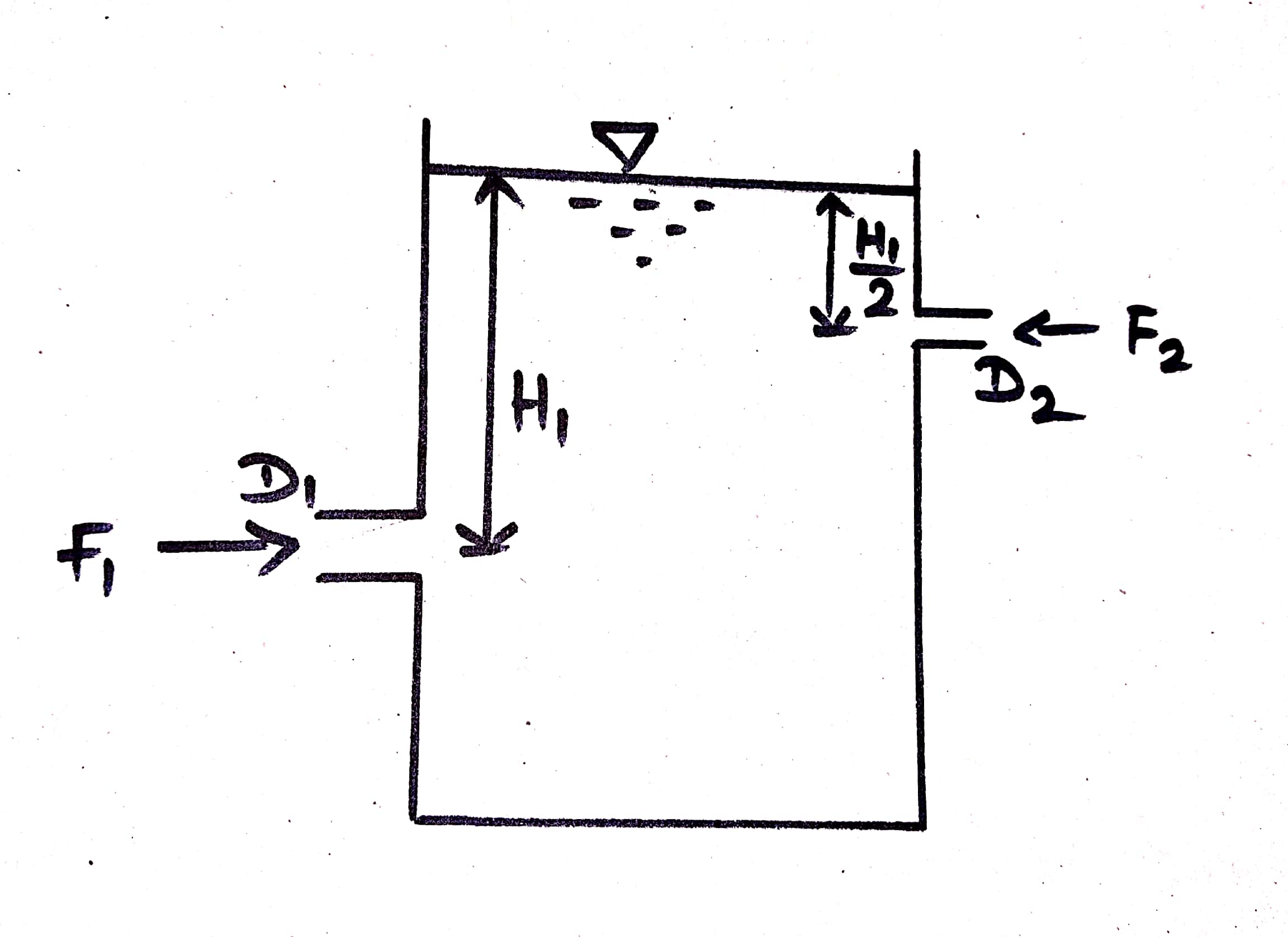
8. A tank has a nizzle of exit diameter `D_1` at a depth `H_1` below free surface. At side opposite to that of nozzle 1, anor nozzle is proposed at a depth `H_1/2`. What should be diameter `D_2` in terms of diameter `D_1` so that net horizontal force on tank is zero?
SOLUTION:
Let,
`F_1` be the force due to nozzle 1
`F_2` be the force due to nozzle 2
For `D_1`,
`F_1=d/(dt)(mV)`
`=rho*Q*V`
`=rho*A_1*(V_1)^2`
`=(pi rho)/4*(D_1)^2*(V_1)^2`... (i)
Similarly the force due to nozzle 2 is,
`F_2=(pi rho)/4*(D_2)^2*(V_2)^2`... (ii)
Also,
`V_1=root ()(2gH_1)`
And `V_2=root ()(2gH_2)`
Since `H_2=H_1/2`,
`V_2=root ()(gH_1)`
According to questions,
`F_1=F_2`
`(D_1)^2*(V_1)^2=(D_2)^2*(V_2)^2`
`(D_1)^2*(2gH_1)=(D_2)^2*(gH_1)`
`D_2=root ()(2)*D_1`
`D_2=1.414D_1`
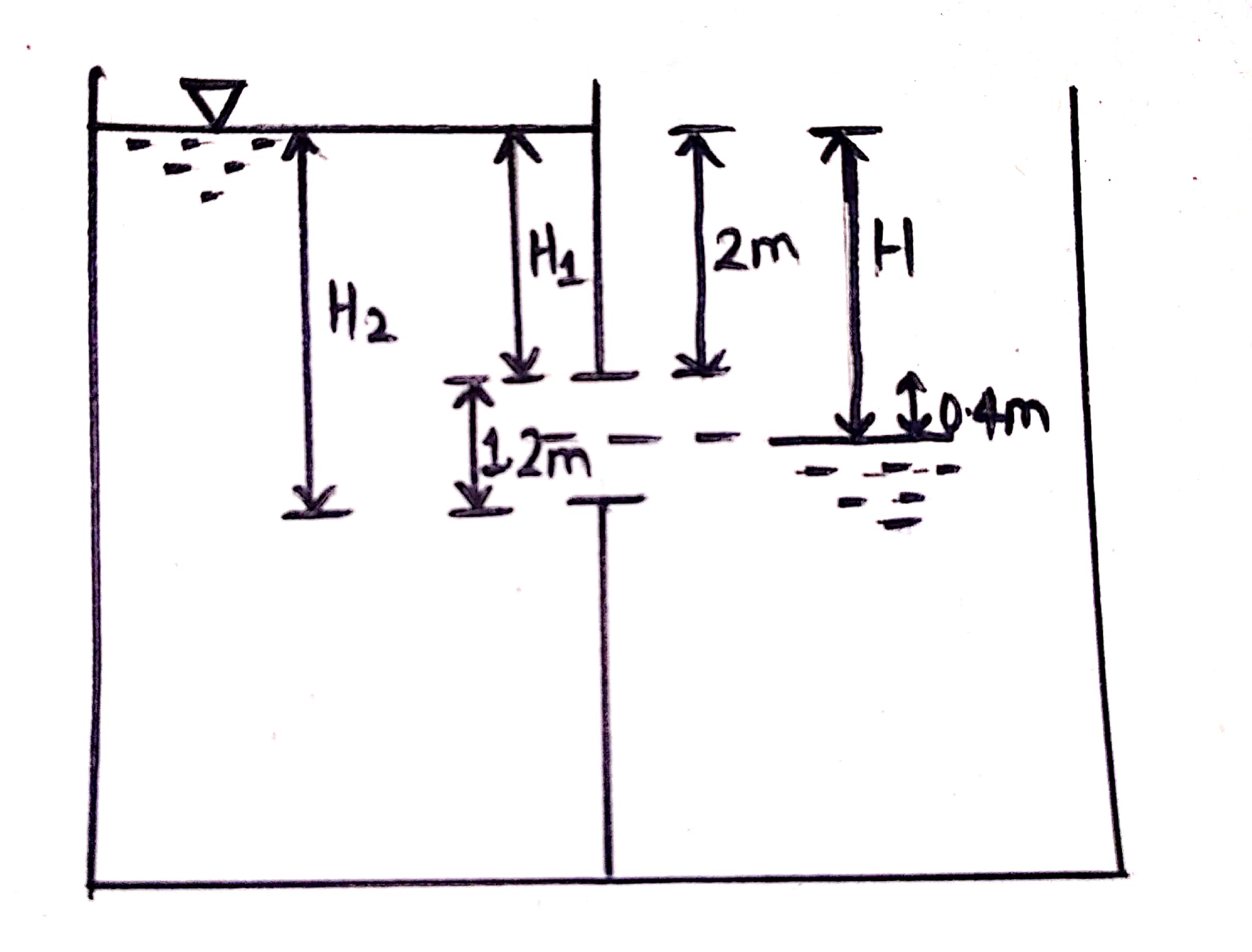
9. A rectangular orifice 1.5m wide and 1.2 m deep is fitted in one side of a large tank. The water level on one side of orifice is 2m above top edge of orifice while on or side of orifice, water level is 0.4m below its top edge. Calculate discharge through orifice if `c_d` is 0.62.
SOLUTION:
Here,
Discharge through submerged portion is,
`Q_1=C_d**b (H_2-H)root ()(2gH)`.. (i)
And the discharge through the free portion is,
`Q_2=2/3C_d*b*root ()(2g)(H^(3/2) -(H_1)^(3/2)`.. (ii)
Thus the total discharge is,
`Q=Q_1+Q_2`
`=C_d**b (H_2-H)root ()(2gH)+2/3C_d*b*root ()(2g)(H^(3/2) -(H_1)^(3/2)`
`=5.1+2.44`
`=7.54m^3/s`
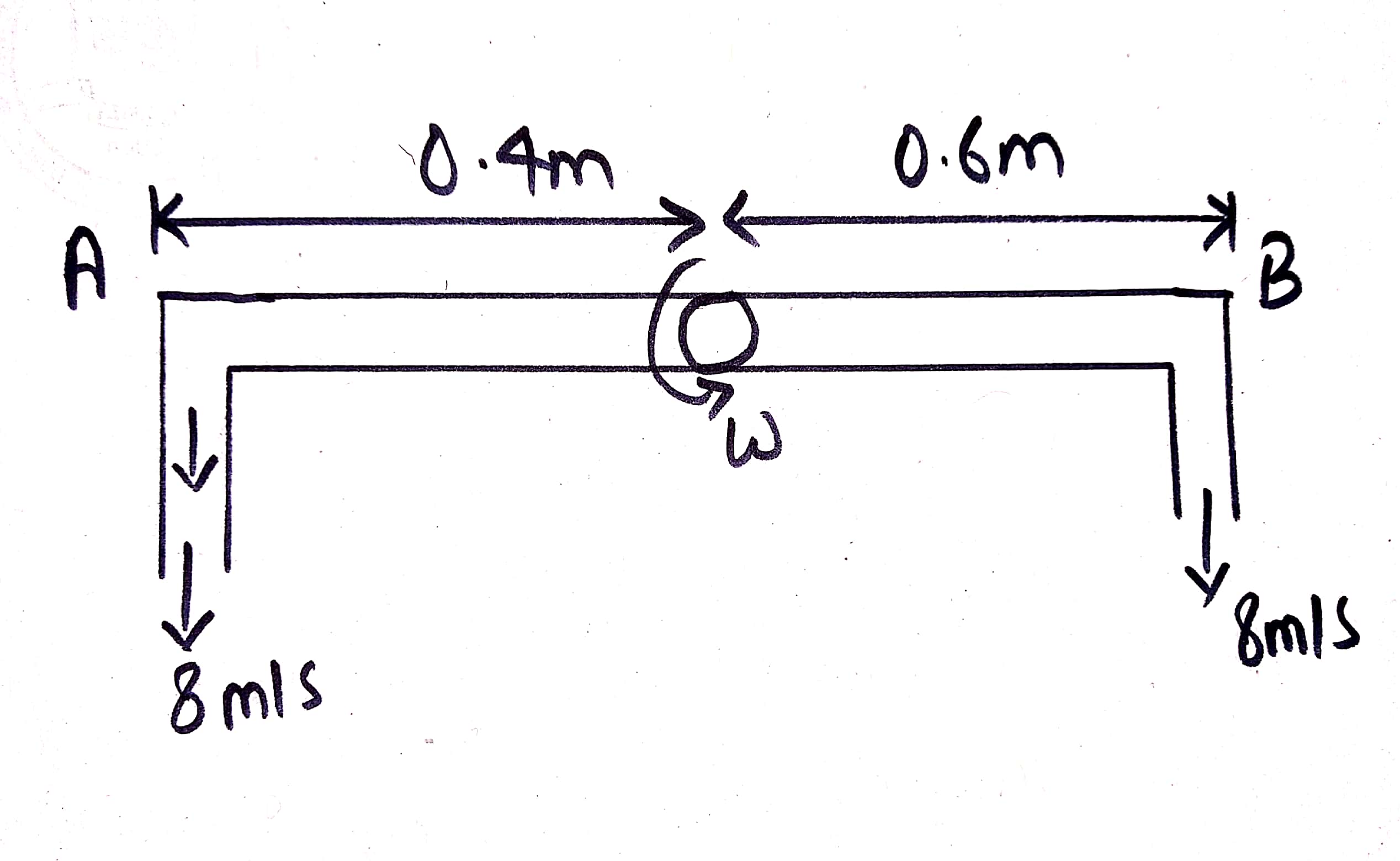
10. Figure shows an unsymmetrical sprinkle. It has a frictionless shaft and equal flow through each nozzle with a velocity of 8 m/s relative to nozzle. Find speed of rotation in r.p.m.
SOLUTION:
Given,
`r_A=0.4m`
`r_B=0.6 m`
Velocity relative to the nozzle,`V_A=V_B=8`m/s
Let `omega` be the angular velocity of the sprinkle.
Now,
Absolute velocity,`V_1=V_A+omega*r_A`
`V_1=8+0.4omega` (positive because the tangential velocity is acting in the same direction as flow velocity )
Similarly, absolute velocity at point B is,
`V_2=V_B-omegar_B`
`V_2=8-0.6omega` (negative because the tangential velocity is acting in opposite direction to the flow velocity )
Now the torque exerted by water coming out at sprinkler A is,
`=rho*Q*V_1*r_1`
This acts in clockwise direction.
Similarly, the torque exerted by water coming out at sprinkler B is,
`=rho*Q*V_2*r_2`
This acts in anticlockwise direction.
Since the moment of the momentum of flow entering is zero and no external torque is applied on the sprinkle, the resultant torque must be zero.i.e,
`T_r=0`
or,`rho*Q (V_2r_2-V_1r_1)=0`
or,`V_2*r_2=V_1*r_1`
or,`(8+0.4omega)**0.4=(8-0.6omega)**0.6`
or,`omega=3.077`rad/s
or,`omega=3.077**60/(2pi)`
or`omega=29.4 r p m`
All Chapters
Dimensional Analysis, Similitude and Physical Modelling
Flow Past Through Submerged Body
Boundary Layer Theory
Properties of fluid
- properties of fluids
- complete IOE solution on fluid mechanics
- Detailed description chapterwise
- Unlimited Numericals problem solved with updation daily
- And much more
Hydrostatics
- Hydrostatics basic theory
- All important Numericals
- IOE,PU, MIT,A.M.I.E,Delhi university,EUPS,Engineering service exam solved problems
- Detailed explanation
Hydrostatics- Buoyancy and metacentric height
- detailed explanation of force of buoyancy, metacentric height,stability of floating body
- unlimited numericals solved with updation weekly
- including IOE , PU, KU, GATE, MIT, ANNA UNIVERSITY,UPSC EXAM SOLUTIONS
- And much more
 Guest
Guest